Acronym	gircope, K-4.125
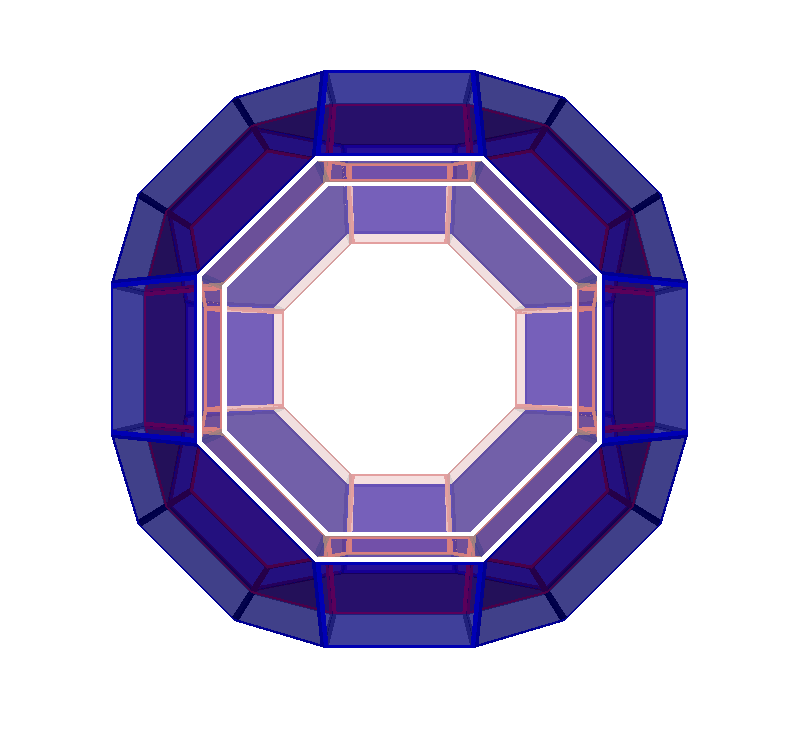
Name	great-rhombicuboctahedron prism
Segmentochoron display
Cross sections	©
Circumradius	sqrt[(7+3 sqrt(2))/2] = 2.370932
Coordinates	((1+2 sqrt(2))/2, (1+sqrt(2))/2, 1/2, 1/2)   & all permutations in all but last coord., all changes of sign
Dihedral angles	at {4} between cube and hip:   arccos[-sqrt(2/3)] = 144.735610° at {4} between cube and op:   135° at {4} between hip and op:   arccos[-1/sqrt(3)] = 125.264390° at {4} between cube and girco:   90° at {6} between girco and hip:   90° at {8} between girco and op:   90°
Face vector	96, 192, 124, 28
Confer	blends: sirpdo   general polytopal classes: Wythoffian polychora   segmentochora
External links

As abstract polytope gircope is isomorphic to quitcope, thereby replacing octagons by octagrams, resp. replacing op by stop and girco by quitco.

The blend of 4 gircopes results in sirpdo.

Incidence matrix according to Dynkin symbol

x x3x4x

. . . . | 96 |  1  1  1  1 |  1  1  1  1  1  1 | 1  1 1 1
--------+----+-------------+-------------------+---------
x . . . |  2 | 48  *  *  * |  1  1  1  0  0  0 | 1  1 1 0
. x . . |  2 |  * 48  *  * |  1  0  0  1  1  0 | 1  1 0 1
. . x . |  2 |  *  * 48  * |  0  1  0  1  0  1 | 1  0 1 1
. . . x |  2 |  *  *  * 48 |  0  0  1  0  1  1 | 0  1 1 1
--------+----+-------------+-------------------+---------
x x . . |  4 |  2  2  0  0 | 24  *  *  *  *  * | 1  1 0 0
x . x . |  4 |  2  0  2  0 |  * 24  *  *  *  * | 1  0 1 0
x . . x |  4 |  2  0  0  2 |  *  * 24  *  *  * | 0  1 1 0
. x3x . |  6 |  0  3  3  0 |  *  *  * 16  *  * | 1  0 0 1
. x . x |  4 |  0  2  0  2 |  *  *  *  * 24  * | 0  1 0 1
. . x4x |  8 |  0  0  4  4 |  *  *  *  *  * 12 | 0  0 1 1
--------+----+-------------+-------------------+---------
x x3x . ♦ 12 |  6  6  6  0 |  3  3  0  2  0  0 | 8  * * *
x x . x ♦  8 |  4  4  0  4 |  2  0  2  0  2  0 | * 12 * *
x . x4x ♦ 16 |  8  0  8  8 |  0  4  4  0  0  2 | *  * 6 *
. x3x4x ♦ 48 |  0 24 24 24 |  0  0  0  8 12  6 | *  * * 2

snubbed forms: x2s3s4x, x s3s4s, s2x3x4s, s2s3s4x, s2s3s4s

xx3xx4xx&#x   → height = 1
(girco || girco)

o.3o.4o.    | 48  * |  1  1  1  1  0  0  0 | 1  1 1  1  1  1 0  0 0 | 1 1  1 1 0
.o3.o4.o    |  * 48 |  0  0  0  1  1  1  1 | 0  0 0  1  1  1 1  1 1 | 0 1  1 1 1
------------+-------+----------------------+------------------------+-----------
x. .. ..    |  2  0 | 24  *  *  *  *  *  * | 1  1 0  1  0  0 0  0 0 | 1 1  1 0 0
.. x. ..    |  2  0 |  * 24  *  *  *  *  * | 1  0 1  0  1  0 0  0 0 | 1 1  0 1 0
.. .. x.    |  2  0 |  *  * 24  *  *  *  * | 0  1 1  0  0  1 0  0 0 | 1 0  1 1 0
oo3oo4oo&#x |  1  1 |  *  *  * 48  *  *  * | 0  0 0  1  1  1 0  0 0 | 0 1  1 1 0
.x .. ..    |  0  2 |  *  *  *  * 24  *  * | 0  0 0  1  0  0 1  1 0 | 0 1  1 0 1
.. .x ..    |  0  2 |  *  *  *  *  * 24  * | 0  0 0  0  1  0 1  0 1 | 0 1  0 1 1
.. .. .x    |  0  2 |  *  *  *  *  *  * 24 | 0  0 0  0  0  1 0  1 1 | 0 0  1 1 1
------------+-------+----------------------+------------------------+-----------
x.3x. ..    |  6  0 |  3  3  0  0  0  0  0 | 8  * *  *  *  * *  * * | 1 1  0 0 0
x. .. x.    |  4  0 |  2  0  2  0  0  0  0 | * 12 *  *  *  * *  * * | 1 0  1 0 0
.. x.4x.    |  8  0 |  0  4  4  0  0  0  0 | *  * 6  *  *  * *  * * | 1 0  0 1 0
xx .. ..&#x |  2  2 |  1  0  0  2  1  0  0 | *  * * 24  *  * *  * * | 0 1  1 0 0
.. xx ..&#x |  2  2 |  0  1  0  2  0  1  0 | *  * *  * 24  * *  * * | 0 1  0 1 0
.. .. xx&#x |  2  2 |  0  0  1  2  0  0  1 | *  * *  *  * 24 *  * * | 0 0  1 1 0
.x3.x ..    |  0  6 |  0  0  0  0  3  3  0 | *  * *  *  *  * 8  * * | 0 1  0 0 1
.x .. .x    |  0  4 |  0  0  0  0  2  0  2 | *  * *  *  *  * * 12 * | 0 0  1 0 1
.. .x4.x    |  0  8 |  0  0  0  0  0  4  4 | *  * *  *  *  * *  * 6 | 0 0  0 1 1
------------+-------+----------------------+------------------------+-----------
x.3x.4x.    ♦ 48  0 | 24 24 24  0  0  0  0 | 8 12 6  0  0  0 0  0 0 | 1 *  * * *
xx3xx ..&#x ♦  6  6 |  3  3  0  6  3  3  0 | 1  0 0  3  3  0 1  0 0 | * 8  * * *
xx .. xx&#x ♦  4  4 |  2  0  2  4  2  0  2 | 0  1 0  2  0  2 0  1 0 | * * 12 * *
.. xx4xx&#x ♦  8  8 |  0  4  4  8  0  4  4 | 0  0 1  0  4  4 0  0 1 | * *  * 6 *
.x3.x4.x    ♦  0 48 |  0  0  0  0 24 24 24 | 0  0 0  0  0  0 8 12 6 | * *  * * 1