 ©
©
| Layer | Symmetry | Subsymmetries | ||
| id × A3 | o3o3o | |||
| 1 | o3x3o top oct | |||
| 2 | o3f3x | |||
| 3 | x3o3F | |||
| 4 | f3x3x bottom (f,x,x)-toe | |||
| Acronym | ... | ||||||||||||||||
| Name | ooxf3xfox3oxFx&#xt | ||||||||||||||||
 © ©
| |||||||||||||||||
| Vertex layers |
| ||||||||||||||||
| Face vector | 54, 150, 128, 32 | ||||||||||||||||
| Confer | |||||||||||||||||
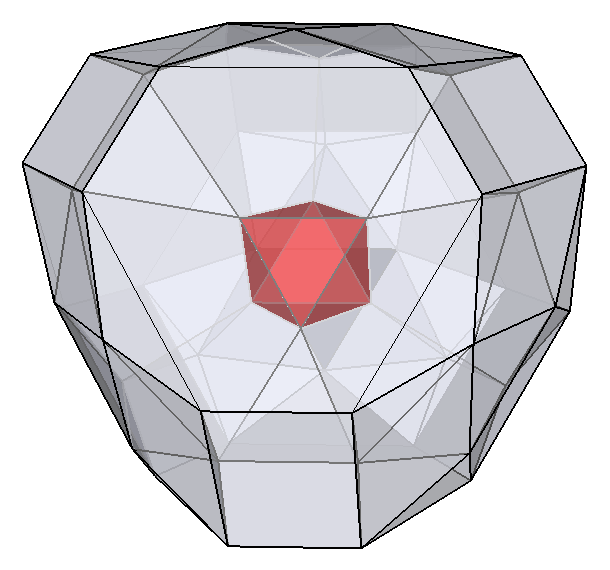
This polychoron was brought up here in mid of 2018. Erroniously the final layer then first had been considered to be x3x3x. But that does not conform with the required hight ratio pattern f:x:f of to be used unbroken flat thawroes. The according recovery then asks for the above mentioned f sized edges in that layer. But then this polytope disqualifies to be a CRF right therefore after all. In fact, those required larger edges are clearly spottable in the picture. – None the less it can be brought back to CRF by continuation beyond that layer. In fact there are various such extensions known, cf. all the B2+## ones.
Incidence matrix according to Dynkin symbol
ooxf3xfox3oxFx&#xt → height(1,2) = height(3,4) = 1/sqrt(8) = 0.353553
height(2,3) = sqrt[3-sqrt(5)]/4 = 0.218508
o...3o...3o... | 6 * * * | 4 2 0 0 0 0 0 0 0 0 | 2 2 4 1 0 0 0 0 0 0 0 0 0 0 | 1 2 2 0 0 0 0
.o..3.o..3.o.. | * 12 * * | 0 1 1 2 2 0 0 0 0 0 | 0 0 2 1 1 1 2 2 0 0 0 0 0 0 | 0 1 2 1 1 0 0
..o.3..o.3..o. | * * 12 * | 0 0 0 2 0 2 2 0 0 0 | 0 0 1 0 2 0 0 2 1 2 1 0 0 0 | 0 1 1 2 0 1 0
...o3...o3...o | * * * 24 | 0 0 0 0 1 0 1 1 1 1 | 0 0 0 0 0 1 1 1 0 1 1 1 1 1 | 0 0 1 1 1 1 1
-------------------+------------+------------------------------+------------------------------------+---------------
.... x... .... | 2 0 0 0 | 12 * * * * * * * * * | 1 1 1 0 0 0 0 0 0 0 0 0 0 0 | 1 1 1 0 0 0 0
oo..3oo..3oo..&#x | 1 1 0 0 | * 12 * * * * * * * * | 0 0 2 1 0 0 0 0 0 0 0 0 0 0 | 0 1 2 0 0 0 0
.... .... .x.. | 0 2 0 0 | * * 6 * * * * * * * | 0 0 0 1 0 0 2 0 0 0 0 0 0 0 | 0 0 2 0 1 0 0
.oo.3.oo.3.oo.&#x | 0 1 1 0 | * * * 24 * * * * * * | 0 0 1 0 1 0 0 1 0 0 0 0 0 0 | 0 1 1 1 0 0 0
.o.o3.o.o3.o.o&#x | 0 1 0 1 | * * * * 24 * * * * * | 0 0 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 1 1 1 0 0
..x. .... .... | 0 0 2 0 | * * * * * 12 * * * * | 0 0 0 0 1 0 0 0 1 1 0 0 0 0 | 0 1 0 1 0 1 0
..oo3..oo3..oo&#x | 0 0 1 1 | * * * * * * 24 * * * | 0 0 0 0 0 0 0 1 0 1 1 0 0 0 | 0 0 1 1 0 1 0
...x .... .... | 0 0 0 2 | * * * * * * * 12 * * | 0 0 0 0 0 1 0 0 0 1 0 1 1 0 | 0 0 0 1 1 1 1
.... ...x .... | 0 0 0 2 | * * * * * * * * 12 * | 0 0 0 0 0 0 0 0 0 0 1 1 0 1 | 0 0 1 0 0 1 1
.... .... ...x | 0 0 0 2 | * * * * * * * * * 12 | 0 0 0 0 0 0 1 0 0 0 0 0 1 1 | 0 0 1 0 1 0 1
-------------------+------------+------------------------------+------------------------------------+---------------
o...3x... .... | 3 0 0 0 | 3 0 0 0 0 0 0 0 0 0 | 4 * * * * * * * * * * * * * | 1 1 0 0 0 0 0
.... x...3o... | 3 0 0 0 | 3 0 0 0 0 0 0 0 0 0 | * 4 * * * * * * * * * * * * | 1 0 1 0 0 0 0
.... xfo. ....&#xt | 2 2 1 0 | 1 2 0 2 0 0 0 0 0 0 | * * 12 * * * * * * * * * * * | 0 1 1 0 0 0 0
.... .... ox..&#x | 1 2 0 0 | 0 2 1 0 0 0 0 0 0 0 | * * * 6 * * * * * * * * * * | 0 0 2 0 0 0 0
.ox. .... ....&#x | 0 1 2 0 | 0 0 0 2 0 1 0 0 0 0 | * * * * 12 * * * * * * * * * | 0 1 0 1 0 0 0
.o.x .... ....&#x | 0 1 0 2 | 0 0 0 0 2 0 0 1 0 0 | * * * * * 12 * * * * * * * * | 0 0 0 1 1 0 0
.... .... .x.x&#x | 0 2 0 2 | 0 0 1 0 2 0 0 0 0 1 | * * * * * * 12 * * * * * * * | 0 0 1 0 1 0 0
.ooo3.ooo3.ooo&#x | 0 1 1 1 | 0 0 0 1 1 0 1 0 0 0 | * * * * * * * 24 * * * * * * | 0 0 1 1 0 0 0
..x.3..o. .... | 0 0 3 0 | 0 0 0 0 0 3 0 0 0 0 | * * * * * * * * 4 * * * * * | 0 1 0 0 0 1 0
..xx .... ....&#x | 0 0 2 2 | 0 0 0 0 0 1 2 1 0 0 | * * * * * * * * * 12 * * * * | 0 0 0 1 0 1 0
.... ..ox ....&#x | 0 0 1 2 | 0 0 0 0 0 0 2 0 1 0 | * * * * * * * * * * 12 * * * | 0 0 1 0 0 1 0
...x3...x .... | 0 0 0 6 | 0 0 0 0 0 0 0 3 3 0 | * * * * * * * * * * * 4 * * | 0 0 0 0 0 1 1
...x .... ...x | 0 0 0 4 | 0 0 0 0 0 0 0 2 0 2 | * * * * * * * * * * * * 6 * | 0 0 0 0 1 0 1
.... ...x3...x | 0 0 0 6 | 0 0 0 0 0 0 0 0 3 3 | * * * * * * * * * * * * * 4 | 0 0 1 0 0 0 1
-------------------+------------+------------------------------+------------------------------------+---------------
o...3x...3o... ♦ 6 0 0 0 | 12 0 0 0 0 0 0 0 0 0 | 4 4 0 0 0 0 0 0 0 0 0 0 0 0 | 1 * * * * * *
oox.3xfo. ....&#xt ♦ 3 3 3 0 | 3 3 0 6 0 3 0 0 0 0 | 1 0 3 0 3 0 0 0 1 0 0 0 0 0 | * 4 * * * * *
.... xfox3oxFx&#xt ♦ 3 6 3 6 | 3 6 3 6 6 0 6 0 3 3 | 0 1 3 3 0 0 3 6 0 0 3 0 0 1 | * * 4 * * * *
.oxf .... ....&#x | 0 1 2 2 | 0 0 0 2 2 1 2 1 0 0 | 0 0 0 0 1 1 0 2 0 1 0 0 0 0 | * * * 12 * * * ox of&#x
.o.f .... .x.x&#x | 0 2 0 4 | 0 0 1 0 4 0 0 2 0 2 | 0 0 0 0 0 2 2 0 0 0 0 0 1 0 | * * * * 6 * *
..xf3..ox ....&#x | 0 0 3 6 | 0 0 0 0 0 3 6 3 3 0 | 0 0 0 0 0 0 0 0 1 3 3 1 0 0 | * * * * * 4 *
...f3...x3...x | 0 0 0 24 | 0 0 0 0 0 0 0 12 12 12 | 0 0 0 0 0 0 0 0 0 0 0 4 6 4 | * * * * * * 1 (f,x,x)-toe
© 2004-2026 | top of page |