Acronym	ticcup, K-4.99
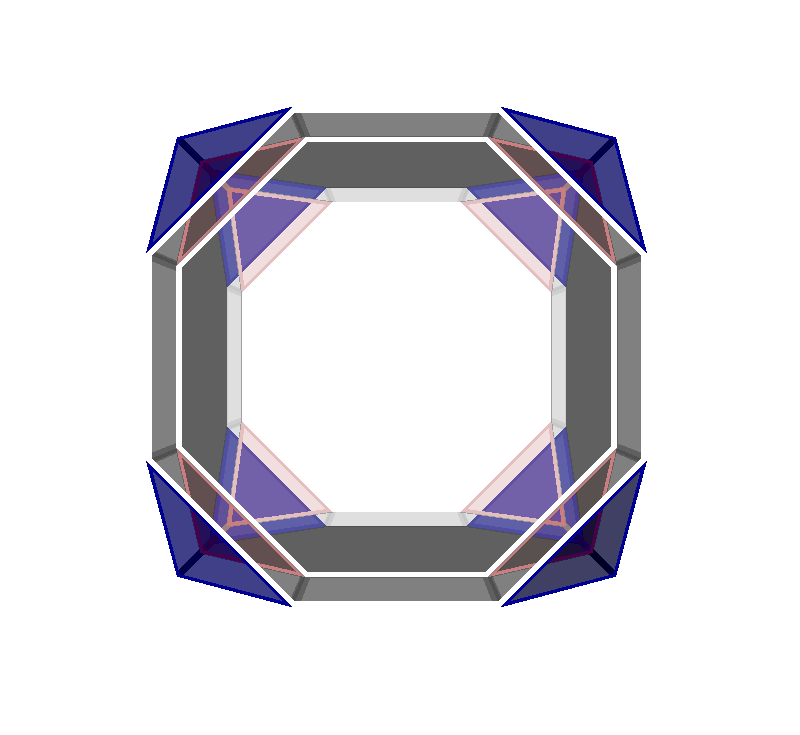
Name	truncated-cube prism
Segmentochoron display
Cross sections	©
Circumradius	sqrt[2+sqrt(2)] = 1.847759
Coordinates	((1+sqrt(2))/2, (1+sqrt(2))/2, 1/2, 1/2)   & all permutations in all but last coord., all changes of sign
Volume	(21+14 sqrt(2))/3 = 13.599663
Dihedral angles	at {4} between op and trip:   arccos[-1/sqrt(3)] = 125.264390° at {4} between op and op:   90° at {8} between op and tic:   90° at {3} between tic and trip:   90°
Face vector	48, 96, 64, 16
Confer	uniform relative: spic   related segmentochora: {4} || op   related CRFs: dapabdi spic   general polytopal classes: Wythoffian polychora   segmentochora
External links

As abstract polytope ticcup is isomorphic to quithip, thereby replacing octagons by octagrams, resp. replacing op by stop and tic by quith.

Ticcup could be gyro-augmented by {4} || op sementochora to obtain dapabdi spic, i.e. the oct-first central bistratic segment of spic. – The prefix "gyro" thereby refers to the chosen orientation of the squares (i.e. the augmentations): being aligned as the co-squares of o3x4o x would be.

Incidence matrix according to Dynkin symbol

x o3x4x

. . . . | 48 |  1  2  1 |  2  1  1  2 | 1 2 1
--------+----+----------+-------------+------
x . . . |  2 | 24  *  * |  2  1  0  0 | 1 2 0
. . x . |  2 |  * 48  * |  1  0  1  1 | 1 1 1
. . . x |  2 |  *  * 24 |  0  1  0  2 | 0 2 1
--------+----+----------+-------------+------
x . x . |  4 |  2  2  0 | 24  *  *  * | 1 1 0
x . . x |  4 |  2  0  2 |  * 12  *  * | 0 2 0
. o3x . |  3 |  0  3  0 |  *  * 16  * | 1 0 1
. . x4x |  8 |  0  4  4 |  *  *  * 12 | 0 1 1
--------+----+----------+-------------+------
x o3x . ♦  6 |  3  6  0 |  3  0  2  0 | 8 * *
x . x4x ♦ 16 |  8  8  8 |  4  4  0  2 | * 6 *
. o3x4x ♦ 24 |  0 24 12 |  0  0  8  6 | * * 2

snubbed forms: s2o3x4s

x o3/2x4x

. .   . . | 48 |  1  2  1 |  2  1  1  2 | 1 2 1
----------+----+----------+-------------+------
x .   . . |  2 | 24  *  * |  2  1  0  0 | 1 2 0
. .   x . |  2 |  * 48  * |  1  0  1  1 | 1 1 1
. .   . x |  2 |  *  * 24 |  0  1  0  2 | 0 2 1
----------+----+----------+-------------+------
x .   x . |  4 |  2  2  0 | 24  *  *  * | 1 1 0
x .   . x |  4 |  2  0  2 |  * 12  *  * | 0 2 0
. o3/2x . |  3 |  0  3  0 |  *  * 16  * | 1 0 1
. .   x4x |  8 |  0  4  4 |  *  *  * 12 | 0 1 1
----------+----+----------+-------------+------
x o3/2x . ♦  6 |  3  6  0 |  3  0  2  0 | 8 * *
x .   x4x ♦ 16 |  8  8  8 |  4  4  0  2 | * 6 *
. o3/2x4x ♦ 24 |  0 24 12 |  0  0  8  6 | * * 2

oo3xx4xx&#x   → height = 1
(tic || tic)

o.3o.4o.    | 24  * |  1  2  1  0  0 | 1 2  2  1 0 0 | 1 1 2 0
.o3.o4.o    |  * 24 |  0  0  1  2  1 | 0 0  2  1 1 2 | 0 1 2 1
------------+-------+----------------+---------------+--------
.. x. ..    |  2  0 | 24  *  *  *  * | 1 1  1  0 0 0 | 1 1 1 0
.. .. x.    |  2  0 |  * 12  *  *  * | 0 2  0  1 0 0 | 1 0 2 0
oo3oo4oo&#x |  1  1 |  *  * 24  *  * | 0 0  2  1 0 0 | 0 1 2 0
.. .x ..    |  0  2 |  *  *  * 24  * | 0 0  1  0 1 1 | 0 1 1 1
.. .. .x    |  0  2 |  *  *  *  * 12 | 0 0  0  1 0 2 | 0 0 2 1
------------+-------+----------------+---------------+--------
o.3x. ..    |  3  0 |  3  0  0  0  0 | 8 *  *  * * * | 1 1 0 0
.. x.4x.    |  8  0 |  4  4  0  0  0 | * 6  *  * * * | 1 0 1 0
.. xx ..&#x |  2  2 |  1  0  2  1  0 | * * 24  * * * | 0 1 1 0
.. .. xx&#x |  2  2 |  0  1  2  0  1 | * *  * 12 * * | 0 0 2 0
.o3.x ..    |  0  3 |  0  0  0  3  0 | * *  *  * 8 * | 0 1 0 1
.. .x4.x    |  0  8 |  0  0  0  4  4 | * *  *  * * 6 | 0 0 1 1
------------+-------+----------------+---------------+--------
o.3x.4x.    ♦ 24  0 | 24 12  0  0  0 | 8 6  0  0 0 0 | 1 * * *
oo3xx ..&#x ♦  3  3 |  3  0  3  3  0 | 1 0  3  0 1 0 | * 8 * *
.. xx4xx&#x ♦  8  8 |  4  4  8  4  4 | 0 1  4  4 0 1 | * * 6 *
.o3.x4.x    ♦  0 24 |  0  0  0 24 12 | 0 0  0  0 8 6 | * * * 1