Acronym tetu
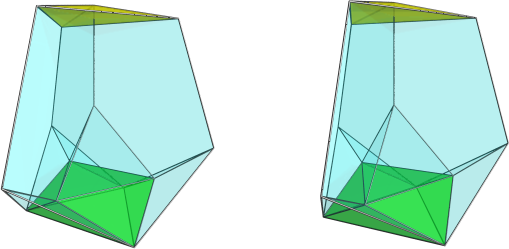
Name axially-tetrahedral ursachoron ofx3xoo3ooo&#xt,
tet-based ursulate,
vertex figure of sadit
  
 ©
 ©      ©
Circumradius 1
Inradius
wrt. tet 		sqrt(5/8) = 0.790569
Inradius
wrt. oct 		1/sqrt(2) = 0.707107
Inradius
wrt. teddi 		[sqrt(5)-1]/4 = 0.309017
Lace city
in approx. ASCII-art 
o o   x x   o o
               
 f o       o f 
               
               
   x o   o x   

    o3o           o3o    
                         
                         
x3o                   x3o
                         
           f3o           
                  o3x
Coordinates
    • (1/sqrt(2), 0, 0; 1/sqrt(2))                                     & all permutations in first 3 coord.s & all changes of sign in first 3 coord.s
    (layer o3x3o in lace tower description resp. top one in lace city)
    • (f/sqrt(8), f/sqrt(8), f/sqrt(8); 1/(F sqrt(8)))            & all even changes of sign in first 3 coord.s
    (layer f3o3o in lace tower description resp. medial one in lace city)
    • (1/sqrt(8), 1/sqrt(8), 1/sqrt(8); -sqrt(5/8))             & all even changes of sign in first 3 coord.s
    (layer x3o3o in lace tower description resp. bottom one in lace city)
where f=(1+sqrt(5))/2, F=ff=f+x   &   circumcenter is at origin
Volume [28+13 sqrt(5)]/96 = 0.594468
Surface [30+9 sqrt(2)+14 sqrt(5)]/12 = 6.169406
Face vector 14, 34, 30, 10
Confer
related CRFs:
octu   iku   coatutu   oct || f-tet || tet || pt   oct || f-tet || dual tet || tet   xfox oxfo3ooox&#xt  
related segmentochora:
{3}||teddi  
general polytopal classes:
ursachora   bistratic lace towers  
analogs:
ursatope Un  
External
links 		polytopewiki   quickfur

The existance of a circumradius shows that this CRF polychoron even is orbiform.

When one of the 4 teddies gets augmented by {3}||teddi (e.g. in the second lace city above at the lower left) then this polychoron becomes xfox oxfo3ooox&#xt (the 3-mibdies-laced wedge).


Incidence matrix according to Dynkin symbol

ofx3xoo3ooo&#xt   → height(1,2) = sqrt[3+sqrt(5)]/4 = 0.572061
                    height(2,3) = sqrt[7+3 sqrt(5)]/4 = 0.925615
(oct || pseudo f-tet || tet)

o..3o..3o..     | 6 * * |  4  2 0 0 | 2 2 1  4 0 | 1 2 2 0
.o.3.o.3.o.     | * 4 * |  0  3 1 0 | 0 0 3  3 0 | 0 3 1 0
..o3..o3..o     | * * 4 |  0  0 1 3 | 0 0 3  0 3 | 0 3 0 1
----------------+-------+-----------+------------+--------
... x.. ...     | 2 0 0 | 12  * * * | 1 1 0  1 0 | 1 1 1 0
oo.3oo.3oo.&#x  | 1 1 0 |  * 12 * * | 0 0 1  2 0 | 0 2 1 0
.oo3.oo3.oo&#x  | 0 1 1 |  *  * 4 * | 0 0 3  0 0 | 0 3 0 0
..x ... ...     | 0 0 2 |  *  * * 6 | 0 0 1  0 2 | 0 2 0 1
----------------+-------+-----------+------------+--------
o..3x.. ...     | 3 0 0 |  3  0 0 0 | 4 * *  * * | 1 1 0 0
... x..3o..     | 3 0 0 |  3  0 0 0 | * 4 *  * * | 1 0 1 0
ofx ... ...&#xt | 1 2 2 |  0  2 2 1 | * * 6  * * | 0 2 0 0
... xo. ...&#x  | 2 1 0 |  1  2 0 0 | * * * 12 * | 0 1 1 0
..x3..o ...     | 0 0 3 |  0  0 0 3 | * * *  * 4 | 0 1 0 1
----------------+-------+-----------+------------+--------
o..3x..3o..     ♦ 6 0 0 | 12  0 0 0 | 4 4 0  0 0 | 1 * * *
ofx3xoo ...&#xt ♦ 3 3 3 |  3  6 3 3 | 1 0 3  3 1 | * 4 * *
... xo.3oo.&#x  ♦ 3 1 0 |  3  3 0 0 | 0 1 0  3 0 | * * 4 *
..x3..o3..o     ♦ 0 0 4 |  0  0 0 6 | 0 0 0  0 4 | * * * 1

© 2004-2024
top of page