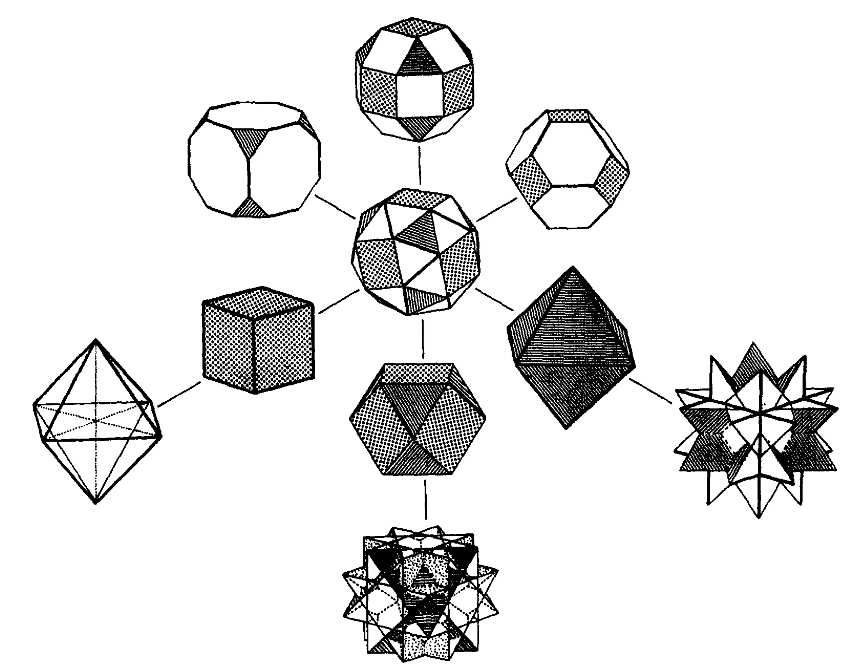
Site Map Polytopes Dynkin Diagrams Vertex Figures, etc. Incidence Matrices Index

Twisters / Gyrohedra / Dipolygonids / Jitterbugs

In 1998 the author got inspired by the fascinating close relationship between polyhedra of type xPoQx, with their vertex configuration [P,4,Q,4], and snub polyhedra of type sPsQs, with their vertex configuration [P,3,Q,3,3], both showing up the face planes of those outstanding P-gons and Q-gons along the same symmetry axis directions.

Only in retrospective he got informed that already nine years before H.F. Verheyen had published "The complete set of jitterbug transformers and the analysis of their motion" a) Comp. Math. Appl., 17, Pergamon, 203-250. Oxford, 1989. b) Symmetry 2: Unifying Human Understanding, ed. I. Hargittai. Pergamon, Oxford, 1989. Therein he called those structures Dipolygonids. Moreover, this research of Verheyen in turn was inspired by the original Jitterbug of R. Buckminster Fuller, who then however had considered the single case P=Q=3 only.

Much later the same topic also became known as Twisters (J. McNeill). In a more greekish way, they well might be dubbed as Gyrohedra, or, if 4D gets involved, Gyrochora too.

The first thing one aims to do here, would be to extend this symmetrical identity of the normal axes of these chosen special faces into a continuous rotation along those, i.e. to have a continuous transformation from the first state of the polygons into the second. For simplicity one discards the filling in rhombisquares of the former or the snub triangles of the latter for now, while focussing on the respective positions and mutual orientations of those P-gons and Q-gons only. Thus one is left with a kind of a polygonal net, spun around the sphere, consisting of alternating P-gons and Q-gons, only stuck together pairwise at their vertices. While the symmetry axes of these remaining polygons are being kept, those outstanding polygons are just twisted around them, say with angles α and β. This transformation then turns out to be a rotation-translation each.

Using the circumradii of those polygons one gets the first connection condition for these angles of rotation in the form 

r(P) sin(α) = r(Q) sin(β)

or, more explicitely, as 

sin(α)/sin(π/P) = sin(β)/sin(π/Q)

Additionally, by introducing the dihedral angle ψ between the face planes of a neighbouring, vertex-connected pair of P-gon and Q-gon, one becomes able to calculate the according axial translation too by means of the height eg. of the P-gon above the polyhedral body centrum as 

h(P) = [r(Q) cos(β)-r(P) cos(α) cos(ψ)]/sin(ψ)

Having introduced the angles α (and β) the deformation has become continuous. Now one gets curious to look beyond the starting and the final points, to see what comes next. Going beyond the starting point (A) of rhombic polyhedra, that is having α<0 degrees, this would generate nothing new, in fact, α'=-α would reproduce the same polyhedra as α, only the right chirality would change into a left chirality (or vice versa).

Going beyond the final point (B) of snubbed polyhedra instead would become more interesting. Here there would come a point (C), where the deformed original squares will degenerate to nothing. This would be the case when the triangles are rotated about 60 degrees or alternatively the pentagrams are rotated about 72 degrees. Drilling even further, the net polygons P and Q would start to intersect and the holes between those become retrograd.

If both net polygons have corner angles which are small enough, there would be further on another interesting point (D), where the deformed holes become again the form of a pair of equilateral triangles, then resulting in an according retrosnub version. But finally you would come to a sudden stop: if the polygon with the smaller corner angle, say P, has been rotated by α=90 degrees.

The trial of rotating still further, that is having α>90 degrees, could be interpreted in different ways. This is due to the fact that there does not exist an inverse function for sine. (One could use the branch of arcsin, but any other as well.) That is, either (a) one jumps over a discontinuity in β from β(α=90-ε) to β(α=90+ε)=180-β(α=90-ε) and could rotate thence both polygons in the same direction as before, or (b) one asks to rotate α still onwards up to 180 degrees but β then would instead be reduced backwards down to 0 degrees again. (Note: in case of P=Q the β-discontinuity in case (a) degenerates, i.e. you are left there with a true bifurcation point!)

However, case (a) not only has that awkward β-discontinuity, it neither will produce anything new: α'=180-α would reproduce exactly the same polyhedra as α, just the way of looking would be retrograde: the inside and outside of those 'net polygons' would simply become interchanged.

Therefore, we are left with the other branch (b). On that branch other things do occur, but those are mostly less interesting than the ones of the first quarter rotation of P. For the Platonic family, for example, only a single highly degenerate intermediate state (B') with coincident faces would come up. For the Keplerian family there are more interesting intermediate states (E), producing uniform polyhedra again. Finally, at rotation α=180 degrees, there would be in any case the last state (A'), where the holes become squares again.

But then again, in the sense of a continuous deformation of according polyhedra, i.e. keeping the same edges connected by according hole-spanning faces while rotation, only cases (A) the exploded form, (B) the outer snub, (C) the closed hole, (D) the inner snub, and (A') the imploded form are relevant. Whereas cases (B') and (E) do ask for different possible closings of those holes!

Concluding:

Symmetry special gyration values       VRML →
o3o3o
case α β result verf
(A) 0° 0° co = x3o3x [3,4,3,4]
(B) 22.239° 22.239° ike = s3s3s [3,3,3,3,3]
(C) 60° 60° oct = o3x3o [3,3,3,3]
(D) 82.239° 82.239° gike = s3/2s3/2s [3,3,3,3,3]/2
(B') 120° 60° comp. of 5 ident. tets [3,3,3] (each)
(A') 180° 0° comp. of 2 ident. thah = x3/2o3x [3/2,4,3,4]

(A)-(B)-(C) 
 ⭳ ©
o3o4o
case α β result verf
(A) 0° 0° sirco = x3o4x [3,4,4,4]
(B) 20.315° 16.468° snic = s3s4s [3,3,3,3,4]
(C) 60° 45° co = o3x4o [3,4,3,4]
(B') 120° 45° comp. of 2 non-ident. thahs
+ 3 ident. octs
(A') 180° 0° querco = x3/2o4x = x3o4/3x [3/2,4,4,4]

(A)-(B)-(C)
o3o5o
case α β result verf
(A) 0° 0° srid = x3o5x [3,4,5,4]
(B) 19.518° 13.106° snid = s3s5s [3,3,3,3,5]
(C) 60° 36° id = o3x5o [3,5,3,5]
(B') 120° 36° comp. of gad + 4 ident. ikes
(A') 180° 0° gicdatrid = x3/2o5x = x3o5/4x 3[3/2,4,5,4]

(A)-(B)-(C)
o5/2o3o
case α β result verf
(A) 0° 0° sicdatrid = x5/2o3x 3[5/2,4,3,4]
(B) 27.108° 24.515° gosid = s5/2s3s [5/2,3,3,3,3]
(C) 72° 60° gid = o5/2x3o [5/2,3,5/2,3]
(D) 88.953° 65.566° girsid = s5/3s3/2s [5/2,3,3,3,3]/2
(E) 108° 60° comp. of sissid + 4 ident. gikes
(B') 133.845° 41.052° gisid = s5/3s3s [5/3,3,3,3,3]
(A') 180° 0° qrid = x5/3o3x = x5/2o3/2x [5/3,4,3,4]

(A)-(B)-(C)


(C)-(B')-(A')
o5/2o5o
case α β result verf
(A) 0° 0° raded = x5/2o5x [5/2,4,5,4]
(B) 23.932° 14.519° siddid = s5/2s5s [5/2,3,5,3,3]
(C) 72° 36° did = o5/2x5o [5/2,5,5/2,5]
(B') 136.388° 25.233° isdid = s5/3s5s [5/3,3,5,3,3]
(A') 180° 0° cadditradid = x5/3o5x = x5/2o5/4x 3[5/3,4,5,4]

(A)-(B)-(C)


(C)-(B')-(A')

Axial Polyhedra
Euclidean Tilings
Polychora
Euclidean Tetracombs

Note, that all those given polychoral or tetracomb cases well could be re-interpreted such, that the s4o-edges, which in step (B) have size |x|=1, would increase towards step (A) into size |q|=sqrt(2), where they just happen to become diagonals of an adjoin of 2 right triangles (aka square) and thus could well be omitted as their diagonals, while towards step (C) those would decrease into size |r|=0, i.e. could be omitted again for a different reason, while some other elements thereby become accordingly coincident.


©

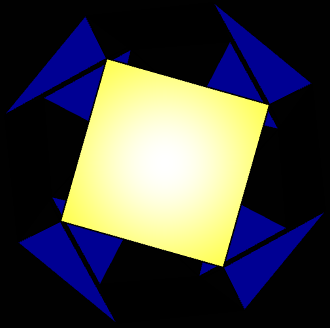
To be fair, it should be admitted, that the purely 3D research of Verheyen then not only considered P,Q > 2, as generally was assumed above, rather he investigated the gyration of degenerate "digonal faces" (i.e. edges) likewise, as can eg. be seen in the diagonal series of his right picture: The vertical series considers various states of gyration of triangle-square dipolygonids, which as such also got described above as states (A) - (B) - (C) - (A'), while the diagonal ones display according states of digon-triangle and digon-square dipolygonids, all of them being considered within the same symmetry group each.

Additionally he also investigated what he dubbed "regular dipolygonids", i.e. coplanar pairs of enantiomorphically gyrating polygons of a single type, i.e. co-axial dipolygonids. E.g. when the pairs of initially coincident squares of 2co would start to gyrate into mutually opposite directions. – On the other hand, his paper of those days fully remained within the 3D spherical geometry only. I.e. ignoring tilings, McNeill's non-uniform 3D applications, and higher-dimensional extrapolations.


Cuned Twisters   (up)

In 2025 a discord member calling himself "Harsin sinquin" came up with what now got called cuneprisms, a series of chiral biform axial polyhedra, then based by concept on a central (chiral isogonal variant of an) antiprism plus lateral, chirally attached wedges. Thereby the lacing zig-zag of the antiprism variant alternates with x-sized (for up) and y-sized (for down) edges, where the x-edges have the same size as the base edges, while the length of the y-edges is free to be adjusted secondarily. The wedges now burry those y-edges underneath, so that the result becomes all unit-edged again. In fact, the requirement that those wedge-triangles all are regular ones as well, thereby settles the size of those (internal) y-edges after all.

When re-considering those under the ideas of this page, it becomes clear, that the set of x-edges of those antiprism variants together with its base faces in fact simply form a o2oNo-twister by means of the varying size of those lateron being burried pseudo y-edges. But having said this, it becomes apparent, that the same construction will apply for oNoMo-twister as well, then likewise resulting in biform polyhedra once more. Below some of these get examplified:

© © © ©
o2o5o o3o3o o3o4o o5/2o5o (etc.)

© 2004-2025
top of page