Acronym	gahi, apD
Name	grand hecatonicosachoron, aggrandized polydodecahedron
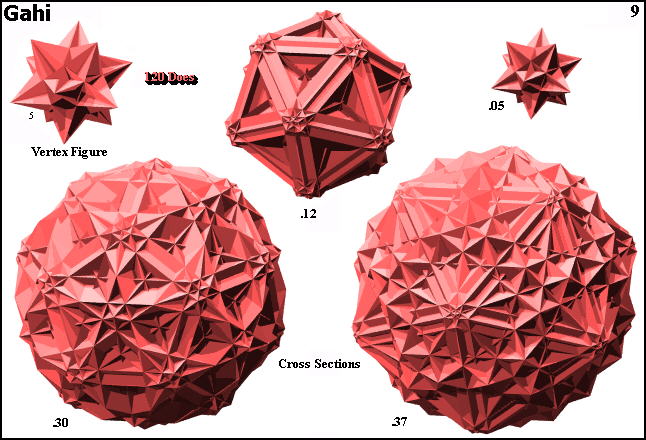
Cross sections	©
Circumradius	(1+sqrt(5))/2 = 1.618034
Inradius	(1+sqrt(5))/4 = 0.809017
Density	20
Coordinates	(τ, 0, 0, 0)             & all permutations, all changes of sign (vertex inscribed f/q-hex) (τ/2, τ/2, τ/2, τ/2)   & all permutations, all changes of sign (vertex inscribed f-tes) (τ2/2, τ/2, 1/2, 0)   & even permutations, all changes of sign (vertex inscribed sadi) where τ = (1+sqrt(5))/2 (a. and b. together define a vertex inscribed f-ico)
General of army	ex
Colonel of regiment	ex
Dual	gishi
Dihedral angles	at {5} between doe and doe:   72°
Face vector	120, 720, 720, 120
Confer	Grünbaumian relatives: fix+gahi+120id   gahi+gohi   2gahi   general polytopal classes: Wythoffian polychora   regular   noble polytopes
External links

As abstract polytope gahi is isomorphic to gishi, thereby replacing doe by gissid, resp. replacing pentagonal faces by pentagrammal ones, resp. replacing pentagrammal edge figures each by pentagonal ones, resp. replacing gike vertex figures by ike ones. – As such gahi is a lieutenant.

Both gahi and gishi can be seen as different realizations of the same self-dual regular abstract polychoron {5,3,5|3} = x5o3o5o | x3o (where the suffix denotes the size of the corresponding hole). In fact, the latter occurs here as face of the circumscribing gike.

Incidence matrix according to Dynkin symbol

x5o3o5/2o

. . .   . | 120 ♦  12 |  30 |  20
----------+-----+-----+-----+----
x . .   . |   2 | 720 |   5 |   5
----------+-----+-----+-----+----
x5o .   . |   5 |   5 | 720 |   2
----------+-----+-----+-----+----
x5o3o   . ♦  20 |  30 |  12 | 120

snubbed forms: β5o3o5/2o

x5o3o5/3o

. . .   . | 120 ♦  12 |  30 |  20
----------+-----+-----+-----+----
x . .   . |   2 | 720 |   5 |   5
----------+-----+-----+-----+----
x5o .   . |   5 |   5 | 720 |   2
----------+-----+-----+-----+----
x5o3o   . ♦  20 |  30 |  12 | 120

x5o3/2o5/2o

. .   .   . | 120 ♦  12 |  30 |  20
------------+-----+-----+-----+----
x .   .   . |   2 | 720 |   5 |   5
------------+-----+-----+-----+----
x5o   .   . |   5 |   5 | 720 |   2
------------+-----+-----+-----+----
x5o3/2o   . ♦  20 |  30 |  12 | 120

x5o3/2o5/3o

. .   .   . | 120 ♦  12 |  30 |  20
------------+-----+-----+-----+----
x .   .   . |   2 | 720 |   5 |   5
------------+-----+-----+-----+----
x5o   .   . |   5 |   5 | 720 |   2
------------+-----+-----+-----+----
x5o3/2o   . ♦  20 |  30 |  12 | 120

x5/4o3o5/2o

.   . .   . | 120 ♦  12 |  30 |  20
------------+-----+-----+-----+----
x   . .   . |   2 | 720 |   5 |   5
------------+-----+-----+-----+----
x5/4o .   . |   5 |   5 | 720 |   2
------------+-----+-----+-----+----
x5/4o3o   . ♦  20 |  30 |  12 | 120

x5/4o3o5/3o

.   . .   . | 120 ♦  12 |  30 |  20
------------+-----+-----+-----+----
x   . .   . |   2 | 720 |   5 |   5
------------+-----+-----+-----+----
x5/4o .   . |   5 |   5 | 720 |   2
------------+-----+-----+-----+----
x5/4o3o   . ♦  20 |  30 |  12 | 120

x5/4o3/2o5/2o

.   .   .   . | 120 ♦  12 |  30 |  20
--------------+-----+-----+-----+----
x   .   .   . |   2 | 720 |   5 |   5
--------------+-----+-----+-----+----
x5/4o   .   . |   5 |   5 | 720 |   2
--------------+-----+-----+-----+----
x5/4o3/2o   . ♦  20 |  30 |  12 | 120

x5/4o3/2o5/3o

.   .   .   . | 120 ♦  12 |  30 |  20
--------------+-----+-----+-----+----
x   .   .   . |   2 | 720 |   5 |   5
--------------+-----+-----+-----+----
x5/4o   .   . |   5 |   5 | 720 |   2
--------------+-----+-----+-----+----
x5/4o3/2o   . ♦  20 |  30 |  12 | 120