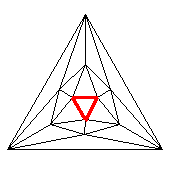
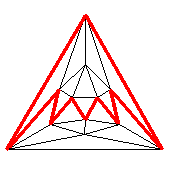
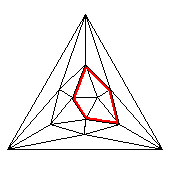
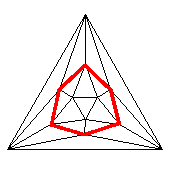
©
Icosahedral graph with emphasized face, Petrie polygon, hole, and 2nd-order Petrie polygon repectively. – Higher ordered ones do not make sense for just 5 faces per vertex.
| Site Map | Polytopes | Dynkin Diagrams | Vertex Figures, etc. | Incidence Matrices | Index |
Usually polygons are considered partially ordered sets, having vertices, edges (sides), and some spanned membran (their area or body). In the early 20th century Coxeter and Petrie came up with the concept of skeletal polygons. There only the vertices and edges remain to be considered, whereas the existance of a spanned (flat) membran is no longer required. This then also allows for non-flat and still regular "polygons" like finite or infinite zig-zags, for infinite helices (with finite flat polygonal projection image), or simply the linear apeirogon.
The best-known skeletal polygons however are the Petrie polygons. Those are defined to be skeletal polygons contained within regular polytopes as pseudo faces, which outlines in d-dimensional subelements a sequence of d+1 consecutive edges and then continues accordingly with the neighbouring d-dimensional subelement, where it already had outlined d consecutive edges. As induction start one clearly can take a flat regular polygon. Here the polygon itself and its Petrie polygon coincides. With respect to polyhedra e.g. the Petrie polygons thus are nothing but the equatorial antiprismatic zig-zags. In fact, these Petrie polygons quite generally are eqatorial non-flat zig-zags, allowing for some projection onto a 2-dimensional subspace. Thereby the polytope then will be contained completely within the projection of that zig-zag, which by itself then becomes a flat convex regular polygon.
E.g. within regular polytopes xPoQo...oRo = {P,Q,...,R} the length S of the respective Petrie polygon sometimes gets emphasized additionally by an according index, i.e. {P,Q,...,R}S. It should be noted here however that the latter symbol on the other hand is also being re-used for according mod-wraps, i.e. polytopes, which have the same local structure as {P,Q,...,R}, but globally get narrowed down to a fraction S' of the former length S by means of according identifications, thus yielding {P,Q,...,R}S', cf. e.g. the elliptical polytopes. (Further such mod-wraps e.g. are considered under the name of regular maps.)
It still took some while until such skeletal polygons where considered to be allowable for polytopal faces too. Rather it is a current topic of interest. The earliest according acception maybe was within the definition of the Petrie dual polyhedra. Those are defined to use the same edge skeleton then the starting regular polyhedron, but replaces the former faces by the respective Petrie polygons. This operation then happens to be involutoric, i.e. twice its application returns to the original polyhedron again. In fact there you simply have {P,Q}Rπ = {R,Q}P, which clearly shows this involutoric behaviour.
But much earlier already such skeletal polygons became acceptable for use within vertex figures. This then became the origin for the skew polytopes. Here all the face polygons still remain flat. One further restricts again for local finiteness, esp. dense vertex figures would not be allowed and therefore infinit skeletal polygons are excluded usually as vertex figures.
Besides the Petrie polygons allone also other polygonal skeletal structures can be considered too. These are (here given wrt. a polyhedral surface tiling):
etc.
©
Icosahedral graph with emphasized face, Petrie polygon, hole, and 2nd-order Petrie polygon repectively. – Higher ordered ones do not make sense for just 5 faces per vertex.
Petrie and Coxeter quite early found 3 regular skew polyhedra, all having flat regular convex faces and finite regular skew polygonal vertex figures. Those all happen to be apeirohedra (infinite count of faces) and show up holes (within common sense), providing higher genus patterns. Coxeter writes {P,Q|R} for such a structure. Here P is the (flat) polygonal type of the faces, Q the (skew) polygonal type of the vertex figures, and R the (flat) polygonal type of the tunnel cross section (hole).
Obviously {P,Q|R} = xPoQo|xRo and (flat) {P,Q} = xPoQo have the same incidence structure. But the former has some further symmetry applied, which circles around the tunnels (holes). In fact, xPoQo|xRo happens to be a modwrap of xPoQo, which occurs by identification of each R-th vertex on each hole (in the above defined sense) of xPoQo, i.e. they additionally ask to have xRo for pseudofaces. At least, as far as such a combination of numbers is realizable. Coxeter provides as according requirement (for a representation within 3-dimensional Euclidean space): 2 sin(π/P) sin(π/Q) = cos(π/R).
The skewness and the regularity of the vertex figure (antiprismatic zigzag) implies that here Q has to be even generally. As xPoQo|xRo and xQoPo|xRo generally come in dual pairs, the same holds true for P. (However degenerate counterexamples will be contained below.)
Generally it happens that such skew representations of infinite regular polyhedra with flat regular polygons not only occur as embeddings within 3-dimensional Euclidean space, but well also within spherical or hyperbolical space of same local dimensionality. In fact an according mod-wrap x(2P)o(2Q)o|xRo generally occurs as a facial substructure of xPxRoQoR*a. And the above mentioned appearance in dual pairings then reflects itself just in the interchange of the node symbol types.
Applying the above general observation, within late 2022 Plasmath found the below mentioned 4 finite modwraps of infinitely dense pre-images.
| infinite ones (within euclidean space) | ||||||
|---|---|---|---|---|---|---|
x4o6o|x4o, mucube (muc)
©
©
dual: x6o4o|x4o 
x4o3o4x (N → ∞) . . . . | 4N | 6 | 3 6 | 2 6 -----------+----+-----+-------+----- x . . . & | 2 | 12N | 2 2 | 1 3 -----------+----+-----+-------+----- x4o . . & | 4 | 4 | 6N * | 1 1 x . . x | 4 | 4 | * 6N | 0 2 -----------+----+-----+-------+----- x4o3o . & ♦ 8 | 12 | 6 0 | N * x4o . x & ♦ 8 | 12 | 2 4 | * 3N |
x6o4o|x4o, muoctahedron (muo)
©
dual: x4o6o|x4o
o4x3x4o (N → ∞) . . . . | 6N | 4 | 2 4 | 4 -----------+----+-----+-------+-- . x . . & | 2 | 12N | 1 2 | 3 -----------+----+-----+-------+-- o4x . . & | 4 | 4 | 3N * | 2 . x3x . | 6 | 6 | * 4N | 2 -----------+----+-----+-------+-- o4x3x . & ♦ 24 | 36 | 6 8 | N |
x6o6o|x3o, mutetrahedron (mut)
©
selfdual
x3x3o3o3*a (N → ∞) . . . . | 2N | 6 | 6 6 | 6 2 --------------+----+----+-------+---- x . . . & | 2 | 6N | 2 2 | 3 1 --------------+----+----+-------+---- x3x . . | 6 | 6 | 2N * | 2 0 x . . o3*a & | 3 | 3 | * 4N | 1 1 --------------+----+----+-------+---- x3x3o . & ♦ 12 | 18 | 4 4 | N * x . o3o3*a & ♦ 4 | 6 | 0 4 | * N |
||||
| finite ones (within spherical space) | ||||||
|
x4o6o|x3o
dual: x6o4o|x3o as substructure of x2x3o3o3*a = x3o3o3x (spid) x3o3o3x . . . . | 20 | 6 | 6 6 | 2 6 -----------+----+----+-------+------ x . . . & | 2 | 60 | 2 2 | 1 3 -----------+----+----+-------+------ x3o . . & | 3 | 3 | 40 * | 1 1 x . . x | 4 | 4 | * 30 | 0 2 -----------+----+----+-------+------ x3o3o . & ♦ 4 | 6 | 4 0 | 10 * x3o . x & ♦ 6 | 9 | 2 3 | * 20 |
x6o4o|x3o
dual: x4o6o|x3o as substructure of x3x3o2o3*a = o3x3x3o (deca) o3x3x3o . . . . | 30 | 4 | 2 4 | 4 -----------+----+----+-------+--- . x . . & | 2 | 60 | 1 2 | 3 -----------+----+----+-------+--- o3x . . & | 3 | 3 | 20 * | 2 . x3x . | 6 | 6 | * 20 | 2 -----------+----+----+-------+--- o3x3x . & ♦ 12 | 18 | 4 4 | 10 |
x4o4o|xRo = regular map {4,4}(R,0)
selfdual as substructure of x2xRo2oR*a = xRo xRo ((R,R)-dip) xRo xRo . . . . | RR | 4 | 2 4 | 4 -----------+----+-----+-------+--- x . . . & | 2 | 2RR | 1 2 | 3 -----------+----+-----+-------+--- xRo . . & | R | R | 2R * | 2 x . x . | 4 | 4 | * RR | 2 -----------+----+-----+-------+--- xRo x . & ♦ 2R | 3R | 2 R | 2R |
||||
|
x4o8o|x3o
dual: x8o4o|x3o as substructure of x2x3o4o3*a = x3o4o3x (spic) x3o4o3x . . . . | 144 | 8 | 8 8 | 2 8 -----------+-----+-----+---------+------- x . . . & | 2 | 576 | 2 2 | 1 3 -----------+-----+-----+---------+------- x3o . . & | 3 | 3 | 384 * | 1 1 x . . x | 4 | 4 | * 288 | 0 2 -----------+-----+-----+---------+------- x3o4o . & ♦ 6 | 12 | 8 0 | 48 * x3o . x & ♦ 6 | 9 | 2 3 | * 192 |
x8o4o|x3o
dual: x4o8o|x3o as substructure of x4x3o2o3*a = o3x4x3o (cont) o3x4x3o . . . . | 288 | 4 | 2 4 | 4 -----------+-----+-----+---------+--- . x . . & | 2 | 576 | 1 2 | 3 -----------+-----+-----+---------+--- o3x . . & | 3 | 3 | 192 * | 2 . x4x . | 8 | 8 | * 144 | 2 -----------+-----+-----+---------+--- o3x4x . & ♦ 24 | 36 | 8 6 | 48 |
x3o8o|x3o
as substructure of o3x3o4o (ico) o3x3o4o . . . . | 24 ♦ 8 | 4 8 | 4 2 --------+----+----+-------+----- . x . . | 2 | 96 | 1 2 | 2 1 --------+----+----+-------+----- o3x . . | 3 | 3 | 32 * | 2 0 . x3o . | 3 | 3 | * 64 | 1 1 --------+----+----+-------+----- o3x3o . ♦ 6 | 12 | 4 4 | 16 * . x3o4o ♦ 6 | 12 | 0 8 | * 8(however this one results in 8 tip-connected octs, i.e. its verf decomposes into 2 unconnected squares) |
||||
|
x4o3o|x4o
dual: x3o4o|x4o as substructure of x2x4o3o = x o3o4x (tes) x o3o4x . . . . | 16 ♦ 1 3 | 3 3 | 3 1 --------+----+------+-------+---- x . . . | 2 | 8 * | 3 0 | 3 0 . . . x | 2 | * 24 | 1 2 | 2 1 --------+----+------+-------+---- x . . x | 4 | 2 2 | 12 * | 2 0 . . o4x | 4 | 0 4 | * 12 | 1 1 --------+----+------+-------+---- x . o4x ♦ 8 | 4 8 | 4 2 | 6 * . o3o4x ♦ 8 | 0 12 | 0 6 | * 2(however this one decomposes into 2 unconnected cubes) |
x3o4o|x4o
dual: x4o3o|x4o as substructure of x2x3o4o = x x3o4o (ope) x x3o4o . . . . | 12 ♦ 1 4 | 4 4 | 4 1 --------+----+------+-------+---- x . . . | 2 | 6 * | 4 0 | 4 0 . x . . | 2 | * 24 | 1 2 | 2 1 --------+----+------+-------+---- x x . . | 4 | 2 2 | 12 * | 2 0 . x3o . | 3 | 0 3 | * 16 | 1 1 --------+----+------+-------+---- x x3o . ♦ 6 | 3 6 | 3 2 | 8 * . x3o4o ♦ 6 | 0 12 | 0 8 | * 2(however this one decomposes into 2 unconnected octs) |
x3o6o|x3o (V=10, cf. below)
as substructure of o3x3o3o (rap) o3x3o3o . . . . | 10 ♦ 6 | 3 6 | 3 2 --------+----+----+-------+---- . x . . | 2 | 30 | 1 2 | 2 1 --------+----+----+-------+---- o3x . . | 3 | 3 | 10 * | 2 0 . x3o . | 3 | 3 | * 20 | 1 1 --------+----+----+-------+---- o3x3o . ♦ 6 | 12 | 4 4 | 5 * . x3o3o ♦ 4 | 6 | 0 4 | * 5(however this one results in 5 tip-connected tets, i.e. its verf decomposes into 2 unconnected triangles) |
||||
|
x4o8/3o|x3o
dual: x8/3o4o|x3o as substructure of x2x3o4/3o3*a = x3o4/3o3x (quippic) x3o4/3o3x . . . . | 144 | 8 | 8 8 | 2 8 -------------+-----+-----+---------+------- x . . . & | 2 | 576 | 2 2 | 1 3 -------------+-----+-----+---------+------- x3o . . & | 3 | 3 | 384 * | 1 1 x . . x | 4 | 4 | * 288 | 0 2 -------------+-----+-----+---------+------- x3o4/3o . & ♦ 6 | 12 | 8 0 | 48 * x3o . x & ♦ 6 | 9 | 2 3 | * 192(note that the pre-image x4o8/3o of this mod-wrap would be an infinitely dense polyhedron) |
x8/3o4o|x3o
dual: x4o8/3o|x3o as substructure of x4/3x3o2o3*a = o3x4/3x3o (gic) o3x4/3x3o . . . . | 288 | 4 | 2 4 | 4 -------------+-----+-----+---------+--- . x . . & | 2 | 576 | 1 2 | 3 -------------+-----+-----+---------+--- o3x . . & | 3 | 3 | 192 * | 2 . x4/3x . | 8 | 8 | * 144 | 2 -------------+-----+-----+---------+--- o3x4/3x . & ♦ 24 | 36 | 8 6 | 48(note that the pre-image o4o8/3x of this mod-wrap would be an infinitely dense polyhedron) |
x8o8/3o|x3o
dual: x8/3o8o|x3o as substructure of x4x3o4/3o3*a = x3o4/3o3x4*a (siddic) x3o4/3o3x4*a . . . . | 144 | 8 | 8 8 | 2 8 ----------------+-----+-----+---------+------ x . . . & | 2 | 576 | 2 2 | 1 3 ----------------+-----+-----+---------+------ x3o . . & | 3 | 3 | 384 * | 1 1 x . . x4*a | 8 | 8 | * 144 | 0 2 ----------------+-----+-----+---------+------ x3o4/3o . & ♦ 6 | 12 | 8 0 | 48 * x3o . x4*a & ♦ 24 | 36 | 8 6 | * 48(note that the pre-image x8o8/3o of this mod-wrap would be an infinitely dense flat tiling) |
||||
|
x8/3o8o|x3o
dual: x8o8/3o|x3o as substructure of x4/3x3o4o3*a = x3o4o3x4/3*a (giddic) x3o4o3x4/3*a . . . . | 144 | 8 | 8 8 | 2 8 ----------------+-----+-----+---------+------ x . . . & | 2 | 576 | 2 2 | 1 3 ----------------+-----+-----+---------+------ x3o . . & | 3 | 3 | 384 * | 1 1 x . . x4/3*a | 8 | 8 | * 144 | 0 2 ----------------+-----+-----+---------+------ x3o4o . & ♦ 6 | 12 | 8 0 | 48 * x3o . x4/3*a & ♦ 24 | 36 | 8 6 | * 48(note that the pre-image o8o8/3x of this mod-wrap would be an infinitely dense flat tiling) |
x3o6o|x3o (V=8, cf. above)
(below mentioned as red/blue {4}) become displayed as the parallel bases of a 3D squap. Despite its asymmetrical representation of this projection, within 4D all triangles are regular. acc. to 2 alternate Möbius-Kantor polygonal substructures of x3o3o4o (hex)
4 * | 2 2 2 0 | 2 4 2 1 2 1 | 4 4 r4b2 vertices
* 4 | 0 2 2 2 | 1 2 1 2 4 2 | 4 4 r2b4 vertices
----+---------+-------------+----
2 0 | 4 * * * | 1 2 1 0 0 0 | 2 2 red {4}'s sides
1 1 | * 8 * * | 1 1 0 1 1 0 | 3 1 red {8}'s sides
1 1 | * * 8 * | 0 1 1 0 1 1 | 1 3 blue {8/3}'s sides
0 2 | * * * 4 | 0 0 0 1 2 1 | 2 2 blue {4}'s sides
----+---------+-------------+----
2 1 | 1 2 0 0 | 4 * * * * * | 2 0 {(rrr)}
2 1 | 1 1 1 0 | * 8 * * * * | 1 1 {(rrb)} at red {4}'s side
2 1 | 1 0 2 0 | * * 4 * * * | 0 2 {(rbb)} at red {4}'s side
1 2 | 0 2 0 1 | * * * 4 * * | 2 0 {(rrb)} at blue {4}'s side
1 2 | 0 1 1 1 | * * * * 8 * | 1 1 {(rbb)} at blue {4}'s side
1 2 | 0 0 2 1 | * * * * * 4 | 0 2 {(bbb)}
----+---------+-------------+----
2 2 | 1 3 1 1 | 1 1 0 1 1 0 | 8 * tet from 4 consec. {8}'s vert.
2 2 | 1 1 3 1 | 0 1 1 0 1 1 | * 8 tet from 4 consec. {8/3}'s vert.
(Note that this hex-derived x3o6o|x3o with 8 vertices obviously is different to therespective rap-derived one with 10 vertices, moreover its verf here does not decompose. Further, although the matrix is given wrt. the 2 substructures, it still is abstractly fully regular.) This "mystic" substructre (as he called it) was found by T. Ruen in February of 2024. |
|||||
| some infinite ones (within hyperbolical space) | ||||||
x4o6o|x5o
©
dual: x6o4o|x5o as substructure of x2x5o3o5*a = x5o3o5x (spidded) x5o3o5x (N → ∞) . . . . | 10N | 6 | 6 6 | 2 6 -----------+-----+-----+---------+----- x . . . & | 2 | 30N | 2 2 | 1 3 -----------+-----+-----+---------+----- x5o . . & | 5 | 5 | 12N * | 1 1 x . . x | 4 | 4 | * 15N | 0 2 -----------+-----+-----+---------+----- x5o3o . & ♦ 20 | 30 | 12 0 | N * x5o . x & ♦ 10 | 15 | 2 5 | * 6N |
x4o6o|x6o
©
as substructure of x2x6o3o6*a = x6o3o6x (spiddihexah) x6o3o6x (N,M → ∞) . . . . | 2NM | 6 | 6 6 | 2 6 -----------+-----+-----+---------+------ x . . . & | 2 | 6NM | 2 2 | 1 3 -----------+-----+-----+---------+------ x6o . . & | 6 | 6 | 2NM * | 1 1 x . . x | 4 | 4 | * 3NM | 0 2 -----------+-----+-----+---------+------ x6o3o . & ♦ 2M | 3M | M 0 | 2N * x6o . x & ♦ 12 | 18 | 2 6 | * NM |
o4o6x|x5o, muicosahedron
©
dual: x4o6o|x5o
o5x3x5o (N → ∞) . . . . | 15N | 4 | 2 4 | 4 -----------+-----+-----+--------+-- . x . . & | 2 | 30N | 1 2 | 3 -----------+-----+-----+--------+-- o5x . . & | 5 | 5 | 6N * | 2 . x3x . | 6 | 6 | * 10N | 2 -----------+-----+-----+--------+-- o5x3x . & ♦ 60 | 90 | 12 20 | N |
||||
|
x6o6o|x4o
selfdual as substructure of x3x4o3o4*a (cytoch) x3x4o3o4*a (N → ∞) . . . . | 4N | 6 | 6 6 | 6 2 --------------+----+-----+-------+---- x . . . & | 2 | 12N | 2 2 | 3 1 --------------+----+-----+-------+---- x3x . . | 6 | 6 | 4N * | 2 0 x . . o4*a & | 4 | 4 | * 6N | 1 1 --------------+----+-----+-------+---- x3x4o . & ♦ 24 | 36 | 8 6 | N * x . o3o4*a & ♦ 8 | 12 | 0 6 | * N |
x8o8o|x3o
selfdual as substructure of o3x4x3o4*a (cytacoh) o3x4x3o4*a (N → ∞) . . . . | 3N | 8 | 8 8 | 8 2 --------------+----+-----+-------+---- . x . . & | 2 | 12N | 2 2 | 3 1 --------------+----+-----+-------+---- o3x . . & | 3 | 3 | 8N * | 1 1 . x4x . | 8 | 8 | * 3N | 2 0 --------------+----+-----+-------+---- o3x4x . & ♦ 24 | 36 | 8 6 | N * o3x . o4*a & ♦ 6 | 12 | 8 0 | * N |
... | ||||
A direct application of Wythoff's construction advice might not be too obvious here. But the according local operations in the sense of Stott expansions surely apply. Because of the existance of skew vertex figures however, this generally would produce not infinite polyhedra with flat faces only. But a single generally applicable exception each could be listed here, none the less. It is the modwrap of x(2P)o(2Q)x, when identifying each 2R-th vertex on each hole. That one then likewise occurs as according facial substructure of xPxRxQxR*a. In fact there it omits, beside all cell bodies for sure, all 2R-gonal faces.
Other infinite polyhedra with flat faces and a single skew vertex figure type only, even when restricted to 3-dimensional eucidean embedding space, so far are still not being classified. Many of them simply are obtained as mirror periodic packings of one ore two uniform polyhedra.
just some examples ...
Just as infinite regular skew polyhedra (those mu-hedra) where obtained from euclidean honeycombs it is straight forward to obtain infinte regular skew polychora (i.e. mu-chora) as substructures of euclidean tetracombs as outlined by Klitzing in 2020. The following first 3 had be derived by the author in those days, the next 2 have been found a year later by D. Sebald. The hyperbolic one has been found by the author within late 2022.
Similar to the 3D case, where {P,Q|R} = xPoQo|xRo described structures with P-gonal faces meeting Q to a vertex with R-gonal pseudofaces, those symbols too could be extrapolated as well. We thus define {P,Q,R|S,T} = xPoQoRo|xSoTo to have {P,Q} = xPoQo cells meeting R to an edge and with {S,T} = xSoTo pseudocells. From the connectivity however it follows that P and S here are bound to have the same value always.
| just some infinite ones (within euclidean space) | ||
|---|---|---|
|
• 16 tets per vertex :
x3o3o4o|o3x4o as substructure of o4x3o3o4o (rittit) o4x3o3o4o (N → ∞) . . . . . | 4N | 12 | 6 24 | 12 16 | 8 2 ----------+----+-----+--------+--------+---- . x . . . | 2 | 24N | 1 4 | 4 4 | 4 1 ----------+----+-----+--------+--------+---- o4x . . . | 4 | 4 | 6N * | 4 0 | 4 0 . x3o . . | 3 | 3 | * 32N | 1 2 | 2 1 ----------+----+-----+--------+--------+---- o4x3o . . ♦ 12 | 24 | 6 8 | 4N * | 2 0 . x3o3o . ♦ 4 | 6 | 0 4 | * 16N | 1 1 ----------+----+-----+--------+--------+---- o4x3o3o . ♦ 32 | 96 | 24 64 | 8 16 | N * . x3o3o4o ♦ 8 | 24 | 0 32 | 0 16 | * Nthe verf of this substructure happens to be x3o4o|x4o. |
• 12 octs per vertex :
x3o4o3o|o3x3o as substructure of o3o4o3x3o (icot) o3o4o3x3o (N → ∞) . . . . . | 12N ♦ 16 | 24 8 | 12 12 | 2 6 ----------+-----+-----+---------+---------+----- . . . x . | 2 | 96N ♦ 3 1 | 3 3 | 1 3 ----------+-----+-----+---------+---------+----- . . o3x . | 3 | 3 | 96N * | 2 1 | 1 2 . . . x3o | 3 | 3 | * 32N | 0 3 | 0 3 ----------+-----+-----+---------+---------+----- . o4o3x . ♦ 6 | 12 | 8 0 | 24N * | 1 1 . . o3x3o ♦ 6 | 12 | 4 4 | * 24N | 0 2 ----------+-----+-----+---------+---------+----- o3o4o3x . ♦ 24 | 96 | 96 0 | 24 0 | N * . o4o3x3o ♦ 24 | 96 | 64 32 | 8 16 | * 3Nthe verf of this substructure happens to be x4o3o|x4o. |
• 64 tets per vertex :
x3o3o8o|x3o3o as substructure of x3o3o *b3o4o (hext) x3o3o *b3o4o (N → ∞) . . . . . | N ♦ 24 | 96 | 32 64 | 16 8 -------------+---+-----+-----+--------+----- x . . . . | 2 | 12N ♦ 8 | 4 8 | 4 2 -------------+---+-----+-----+--------+----- x3o . . . | 3 | 3 | 32N | 1 2 | 2 1 -------------+---+-----+-----+--------+----- x3o3o . . ♦ 4 | 6 | 4 | 8N * | 2 0 x3o . *b3o . ♦ 4 | 6 | 4 | * 16N | 1 1 -------------+---+-----+-----+--------+----- x3o3o *b3o . ♦ 8 | 24 | 32 | 8 8 | 2N * x3o . *b3o4o ♦ 8 | 24 | 32 | 0 16 | * Nthe verf of this substructure happens to be x3o8o|x3o. |
|
• 30 octs per vertex :
x3o4o6o|x3o3o as substructure of x3o3o3o3o3*a (cypit) x3o3o3o3o3*a (N → ∞) . . . . . | N ♦ 20 | 60 | 40 30 | 10 20 ----------------+----+-----+-----+--------+------ x . . . . | 2 | 10N ♦ 6 | 6 6 | 2 6 ----------------+----+-----+-----+--------+------ x3o . . . & | 3 | 3 | 20N | 2 2 | 1 3 ----------------+----+-----+-----+--------+------ x3o3o . . & ♦ 4 | 6 | 4 | 10N * | 1 1 x3o . . o3*a ♦ 6 | 12 | 8 | * 5N | 0 2 ----------------+----+-----+-----+--------+------ x3o3o3o . & ♦ 5 | 10 | 10 | 5 0 | 2N * x3o3o . o3*a & ♦ 10 | 30 | 30 | 5 5 | * 2Nthe verf of this substructure happens to be x4o6o|x3o. |
• 16 octs per vertex :
x3o4o4o|x3o4o as substructure of o4o3x3o4o (icot) o4o3x3o4o (N → ∞) . . . . . | 3N ♦ 16 | 32 | 8 16 | 8 -------------+----+-----+-----+-------+-- . . x . . | 2 | 24N ♦ 4 | 2 4 | 4 -------------+----+-----+-----+-------+-- . o3x . . & | 3 | 3 | 32N | 1 2 | 3 -------------+----+-----+-----+-------+-- o4o3x . . & ♦ 6 | 12 | 8 | 4N * | 2 . o3x3o . ♦ 6 | 12 | 8 | * 8N | 2 -------------+----+-----+-----+-------+-- o4o3x3o . & ♦ 24 | 96 | 96 | 8 16 | Nthe verf of this substructure happens to be x4o4o|x4o. |
|
| finite ones (within spherical space) | ||
|
• 20 tets per vertex :
x3o3o6o|x3o3o as substructure of x3o3o *b3o3o (hin) x3o3o *b3o3o . . . . . | 16 ♦ 10 | 30 | 10 20 | 5 5 -------------+----+----+-----+-------+------ x . . . . | 2 | 80 ♦ 6 | 3 6 | 3 2 -------------+----+----+-----+-------+------ x3o . . . | 3 | 3 | 160 | 1 2 | 2 1 -------------+----+----+-----+-------+------ x3o3o . . ♦ 4 | 6 | 4 | 40 * | 2 0 x3o . *b3o . ♦ 4 | 6 | 4 | * 80 | 1 1 -------------+----+----+-----+-------+------ x3o3o *b3o . ♦ 8 | 24 | 32 | 8 8 | 10 * x3o . *b3o3o ♦ 5 | 10 | 10 | 0 5 | * 16the verf of this substructure happens to be x3o6o|x3o. |
||
| some infinite ones (within hyperbolical space) | ||
|
• 20 trats per vertex :
x3o6o4o|x3o3o as substructure of o3o3o3o *b3x3*c o3o3o3o *b3x3*c (N,M,K → ∞) . . . . . | NMK ♦ 30 | 60 | 20 20 | 10 ------------------+-----+-------+-------+-----------+---- . . . . x | 2 | 15NMK | 4 | 2 4 | 4 ------------------+-----+-------+-------+-----------+---- . o . . *b3x & | 3 | 3 | 20NMK | 1 2 | 3 ------------------+-----+-------+-------+-----------+---- o3o . . *b3x & ♦ 4 | 6 | 4 | 5NMK * | 2 . o3o . *b3x3*c ♦ M | 3M | 2M | * 20NK | 2 ------------------+-----+-------+-------+-----------+---- o3o3o . *b3x3*c & ♦ MK | 6MK | 6MK | MK 4K | 10Nthe verf of this substructure happens to be x6o4o|x3o. |
||
Miss Krieger outlined shortly after those 2020 finds this finite mu-teron.
| just some finite ones (within spherical space) |
|---|
|
• 80 pens per vertex :
x3o3o3o6o|x3o3o3o as substructure of x3o3o3o3o *c3o (jak) x3o3o3o3o *c3o . . . . . . | 27 ♦ 16 | 80 | 160 | 80 40 | 16 10 ---------------+----+-----+-----+------+---------+------ x . . . . . | 2 | 216 ♦ 10 | 30 | 20 10 | 5 5 ---------------+----+-----+-----+------+---------+------ x3o . . . . | 3 | 3 | 720 ♦ 6 | 6 3 | 2 3 ---------------+----+-----+-----+------+---------+------ x3o3o . . . ♦ 4 | 6 | 4 | 1080 | 2 1 | 1 2 ---------------+----+-----+-----+------+---------+------ x3o3o3o . . ♦ 5 | 10 | 10 | 5 | 432 * | 1 1 x3o3o . . *c3o ♦ 5 | 10 | 10 | 5 | * 216 | 0 2 ---------------+----+-----+-----+------+---------+------ x3o3o3o3o . ♦ 6 | 15 | 20 | 15 | 6 0 | 72 * x3o3o3o . *c3o ♦ 10 | 40 | 80 | 80 | 16 16 | * 27the verf of this substructure happens to be x3o3o6o|x3o3o. |
It is quite interesting that the mere surface operation of the honeycomb product ×0,0, when applied to finite polytopal factors rather than infinite euclidean (or even hyperbolic) factors, well generates further (fully dyadic) skew polytopes. This was a topic of interest of T. Ruen in spring of 2023 and Bowers coined their according names to be skewprisms. It is the relation between ×0,1 (the usual cartesian or prism product) and this ×0,0, which again allows to describe those again as substructures of the according prism product of the same factors. However, in here not necessarily a single element type of the last to be considered dimensionality gets rejected, as in the former cases above, rather there might be several ones instead. Also neither the final skew polytope as such nor its facets are regular polytopes any longer.
|
• 6 trips per vertex :
x3o ×0,0 x3o3o, (trig,tet)-skewprism (tratetik) as substructure of x3o x3o3o (tratet) x3o x3o3o . . . . . | 12 | 2 3 | 1 6 3 | 3 6 1 | 3 2 ----------+----+-------+---------+--------+---- x . . . . | 2 | 12 * | 1 3 0 | 3 3 0 | 3 1 . . x . . | 2 | * 18 | 0 2 2 | 1 4 1 | 2 2 ----------+----+-------+---------+--------+---- x3o . . . | 3 | 3 0 | 4 * * | 3 0 0 | 3 0 x . x . . | 4 | 2 2 | * 18 * | 1 2 0 | 2 1 . . x3o . | 3 | 0 3 | * * 12 | 0 2 1 | 1 2 ----------+----+-------+---------+--------+---- x3o x . . ♦ 6 | 6 3 | 2 3 0 | 6 * * | 2 0 x . x3o . ♦ 6 | 3 6 | 0 3 2 | * 12 * | 1 1 . . x3o3o ♦ 4 | 0 6 | 0 0 4 | * * 3 | 0 2 ----------+----+-------+---------+--------+---- x3o x3o . ♦ 9 | 9 9 | 3 9 3 | 3 3 0 | 4 * x . x3o3o ♦ 8 | 4 12 | 0 6 8 | 0 4 2 | * 3the verf of this substructure happens to be oxo3ooo&#qt holes here are the other trips and the tets |
© 2004-2024 | top of page |
