| Site Map | Polytopes | Dynkin Diagrams | Vertex Figures, etc. | Incidence Matrices | Index |
Dihedral angles usually are of interest from a mere external view point. That is, take some polytope and "look" at it from outside. (Whatever such a "looking" would mean within higher dimensions.) From the more internal point of view the aspects of symmetry, and therefore esp. their axes are of primary interest. For uniform polytopes those are given by the fundamental domain. In Wythoffian cases esp. those are what Schläfli once called orthoscheme. Thus it turns out, that the main topic here rather is that of orthoschemometry, those dihedral angles then can be derived easily therefrom.
By the means of Wythoff's kaleidoscopic construction all polytopes with some common symmetry in the sense of an undecorated Dynkin symbol are derived through 2 constituents: the actual kaleidoscope and the seed point. Depending to the position of that seed point with respect to the mirrors of the kaleidoscope (esp. being on or off), the various members of a Wythoffian family are derived. But the symmetry, here represented by the kaleidoscope, does not change for all those family members. So it becomes obvious, that e.g. the dihedral angles between 2 non-degenerate facets across a common margin will be independent of the actual chosen decoration – at least whenever the link marks of the dynkin symbol are all integral (as for fractional cases the relevant inradius depending on the chosen decoration of the symbol occasionally might become negative, and thus the dihedral switches to its complement).
The other constituent, the kaleidoscope, clearly represents what Schläfli was dealing with when introducing the orthoplexes. In fact, the orthoplexes is nothing but the intersection of the (hyper)sphere with that kaleidoscope. That is, for the bounded spherical geometry polytopes of consideration that fundamental domain clearly is a (hyper)spherical simplex indeed. Thus its vertices v(i) are defined by the intersection of D-1 mirrors of the kaleidoscope, its curved edges (ij) = arc(v(i), v(j)) are sustained by some angles β(i,j) at the polytopal body-center, i.e. the tip of the kaleidoscope, between the rays to those vertices, etc. – If R would be the radius for that intersecting (hyper)sphere we'd clearly get (ij) = R β(i,j). In the followings we'll restrict here to an unit radius, i.e. R=1, thus those values become identical when measured in radians.
The Dynkin symbols define by means of the link marks p(i,j) between the i-th and j-th node the submultiplicative numbers of the dihedral angles of the kaleidoscope, i.e. the angles between the thus represented mirrors (hyper)planes m(i) resp. m(j) as π/p(i,j) = ∠ m(i), m(j). (As is known, for generating some repetitive symmetry around that intersection space, those numbers p(i,j) have to be rational at least.) Specific such numbers p(i,j) in the followings will be referred to as p,q,r,... Moreover we'll need quite often the cosines of those kaleidoscopical angles (i.e. the dihedral angles of the orthoplex), so we'd refer to those for short accordingly as P = 4 cos2(π/p), Q = 4 cos2(π/q), R = 4 cos2(π/r), etc. (This definition is in accordance to the shortchords, i.e. P = 4 cos2(π/p) sin2(π/p) / sin2(π/p) = sin2(2π/p) / sin2(π/p) = x2(p,2) = x2(p).) Below the most relevant values:
| p | 2 | 3 | 4 | 5 | 5/2 |
|---|---|---|---|---|---|
| P = 4 cos2(π/p) | 0 | 1 | 2 | (3+sqrt(5))/2 = 2.618034 | (3-sqrt(5))/2 = 0.381966 |

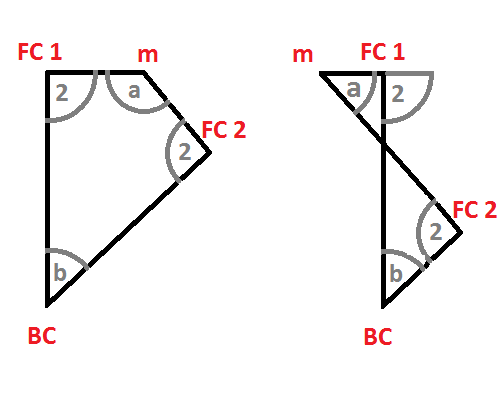
Now to the relation of the dihedral angle α(i,j) of some polytope P at the margin m = P(i,j) between the facets P(i) resp. P(j) (i = j would be allowed here) to the corresponding angle β(i,j) at the body center BC, having legs to the centers of those facets FC(i) resp. FC(j): In general this would be a convex euclidean quatrilatteral, and then one clearly has: α(i,j) = π - β(i,j). But in some spare cases this becomes a crossed quatrilatteral so, where one has α(i,j) = β(i,j) instead. – It is obvious, that for symmetry equivalent facets, i.e. for equal indices, only the former case can occure. The same holds true more general for any index pair in the restriction to convex polytopes only.
---- 2D ----
This case is not only easily accessible, but also to handle here mathematically: we obviously just have (01) = β(0,1) = π/p.
Further we have β(0,0') = β(1,1') = 2 β(0,1) and thus α(0,0') = α(1,1') = π (1 - 2/p).
Because of the equivalence of x-p-x and x-2p-o it becomes obvious moreover, that even more α(0,1) = π (1 - 1/p) would hold as well.
| Symmetry o-p-o |
centri angles | dihedral angles | ||
|---|---|---|---|---|
| p | β(0,0') = β(1,1') |
β(0,1) | α(0,0') = α(1,1') |
α(0,1) |
| 3 | 120° | 60° | 60° | 120° |
| 4 | 90° | 45° | 90° | 135° |
| 5 | 72° | 36° | 108° | 144° |
| 5/2 | 144° | 72° | 36° | 108° |
| 6 | 60° | 30° | 120° | 150° |
| ... | ||||
---- 3D ----
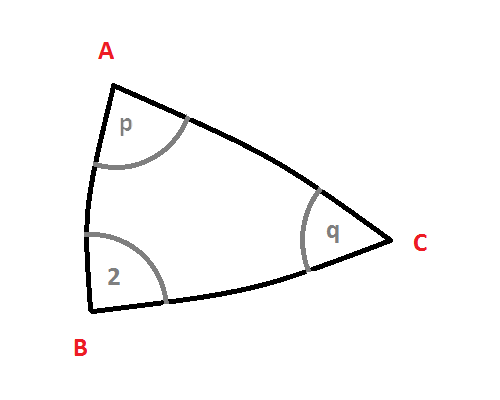
The dual of the orthoscheme of this dimension is known as Schwarz triangle. – To the right (and in the followings) the orthoscheme according to symmetry o-p-o-q-o will be considered. The face, derived by kaleidoscopical construction around vertex A clearly is of subsymmetry o-p-o ., corresponds thus to the omission of the (zero-based) node number 2. By symmetry C corresponds to . o-q-o, or the omission of node 0. The remaining vertex B corresponds to o . o, or to node 1.
Though 3D still is easily accessible, for orthoschemometry this time there have to be some calculations, best to be done by the laws of cosine. Those relate the 3 corner angles U,V,W to the opposite sides u,v,w by
Applying (I) to the right orthoscheme (and using finally the above shortchord definitions P,Q,...) we thus get:
cos(β(0,1)) = cos(BC) =
[cos(π/p) + cos(π/2) cos(π/q)] / [sin(π/2) sin(π/q)] =
cos(π/p) / sin(π/q) =
sqrt[P / (4 - Q)].
Similarily:
cos(β(1,2)) = cos(AB) =
sqrt[Q / (4 - P)].
And either directly by (I), or using (II) one further gets:
cos(β(0,2)) = cos(AC) =
cos(AB) cos(BC) =
sqrt[Q / (4 - P)] sqrt[P / (4 - Q)].
Using cos(2u) = 2 cos2(u) - 1 we thus get: cos(β(0,0)) = cos(2(BC)) = [2P / (4 - Q)] - 1, and similarily: cos(β(2,2)) = cos(2(AB)) = [2Q / (4 - P)] - 1.
For the latter ones we generally have:
cos(α(0,0)) = cos(π - β(0,0)) = - cos(β(0,0)) = 1 - [2P / (4 - Q)], resp.
cos(α(2,2)) = 1 - [2Q / (4 - P)].
In the other index combinations we usually get the followings (i.e. if no retrograde facets contribute):
cos(α(0,1)) =
cos(π - β(0,1)) =
- sqrt[P / (4 - Q)].
Similarily:
cos(α(1,2)) =
cos(π - β(1,2)) =
- sqrt[Q / (4 - P)].
And finally:
cos(α(0,2)) =
cos(π - β(0,2)) =
- sqrt[Q / (4 - P)] sqrt[P / (4 - Q)].
(In retrograde cases we do have for indices i≠j, as already mentioned:
α(i,j) = β(i,j),
and thus would get their values again.)
| Symmetry o-p-o-q-o |
centri angles | |||||
|---|---|---|---|---|---|---|
| p | q | β(0,0') | β(0,1) | β(0,2) | β(1,2) | β(2,2') |
| 3 | 3 | arccos(-1/3) = 109.471221° |
arccos[1/sqrt(3)] = 54.735610° |
arccos(1/3) = 70.528779° |
arccos[1/sqrt(3)] = 54.735610° |
arccos(-1/3) = 109.471221° |
| 3 | 4 | arccos(0) = 90° |
arccos(1/sqrt(2)) = 45° |
arccos[1/sqrt(3)] = 54.735610° |
arccos(sqrt(2/3)) = 35.264390° |
arccos(1/3) = 70.528779° |
| 3 | 5 | arccos(1/sqrt(5)) = 63.434949° |
arccos(sqrt[(5+sqrt(5))/10]) = 31.717474° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
arccos(sqrt[(3+sqrt(5))/6]) = 20.905157° |
arccos(sqrt(5)/3) = 41.810315° |
| 3 | 5/2 | arccos(-1/sqrt(5)) = 116.565051° |
arccos(sqrt[(5-sqrt(5))/10]) = 58.282526° |
arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
arccos(sqrt[(3-sqrt(5))/6]) = 69.094843° |
arccos(-sqrt(5)/3) = 138.189685° |
| 5 | 5/2 | arccos(1/sqrt(5)) = 63.434949° |
arccos(sqrt[(5+sqrt(5))/10]) = 31.717474° |
arccos(1/sqrt(5)) = 63.434949° |
arccos(sqrt[(5-sqrt(5))/10]) = 58.282526° |
arccos(-1/sqrt(5)) = 116.565051° |
| ... | ||||||
| Symmetry o-p-o-q-o |
dihedral angles | |||||
| p | q | α(0,0') | α(0,1) | α(0,2) | α(1,2) | α(2,2') |
| 3 | 3 | arccos(1/3) = 70.528779° |
arccos[-1/sqrt(3)] = 125.264390° |
arccos(-1/3) = 109.471221° |
arccos[-1/sqrt(3)] = 125.264390° |
arccos(1/3) = 70.528779° |
| 3 | 4 | arccos(0) = 90° |
arccos(-1/sqrt(2)) = 135° |
arccos[-1/sqrt(3)] = 125.264390° |
arccos[-sqrt(2/3)] = 144.735610° |
arccos(-1/3) = 109.471221° |
| 3 | 5 | arccos(-1/sqrt(5)) = 116.565051° |
arccos(-sqrt[(5+sqrt(5))/10]) = 148.282526° |
arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(-sqrt[(3+sqrt(5))/6]) = 159.094843° |
arccos(-sqrt(5)/3) = 138.189685° |
| 3 | 5/2 | arccos(1/sqrt(5)) = 63.434949° |
arccos(-sqrt[(5-sqrt(5))/10]) = 121.717474° – or same as β(0,1) |
arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° – or same as β(0,2) |
arccos(-sqrt[(3-sqrt(5))/6]) = 110.905157° – or same as β(1,2) |
arccos(sqrt(5)/3) = 41.810315° |
| 5 | 5/2 | arccos(-1/sqrt(5)) = 116.565051° |
arccos(-sqrt[(5+sqrt(5))/10]) = 148.282526° – or same as β(0,1) |
arccos(-1/sqrt(5)) = 116.565051° – or same as β(0,2) |
arccos(-sqrt[(5-sqrt(5))/10]) = 121.717474° – or same as β(1,2) |
arccos(1/sqrt(5)) = 63.434949° |
| ... | ||||||
(For a detailed list of the relevant Wythoffian polyhedra follow these links to the respective symmetries: o3o3o, o3o4o, o3o5o, o3o5/2o, o3o5/3o, o5o5/2o, o5o5/3o, ...)
Because 3 polygonal faces define a rigid acron (vertex surrounding) one even could calculate the corresponding dihedral angles directly. Thus, given the sides of the spherical triangle on the vertex ball, one easily derives again by the already above given formula cos(u) = cos(v) cos(w) + sin(v) sin(w) cos(U) (law of cosines) the to be determined dihedral angles.
| acron | facial corner angles | dihedral angles | |||||
|---|---|---|---|---|---|---|---|
| vertex figure |
polyhedron example |
α( {p0} ) | α( {p1} ) | α( {p2} ) | α(0,1) | α(0,2) | α(1,2) |
| [3,3,3] | tet | 60° | 60° | 60° | arccos(1/3) = 70.528779° |
arccos(1/3) = 70.528779° |
arccos(1/3) = 70.528779° |
| [3,3,4] | squippy | 60° | 60° | 90° | arccos(-1/3) = 109.471221° |
arccos[1/sqrt(3)] = 54.735610° |
arccos[1/sqrt(3)] = 54.735610° |
| [3,3,5] | peppy | 60° | 60° | 108° | arccos(-sqrt(5)/3) = 138.189685° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
| [3,3,5/2] | stappy | 60° | 60° | 36° | arccos(sqrt(5)/3) = 41.810315° |
arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
| [3,3,8/3] | ogpy | 60° | 60° | 45° | arccos[(sqrt(2)-1)/3] = 52.448397° |
arccos[(2-sqrt(2))/3] = 78.739962° |
arccos[(2-sqrt(2))/3] = 78.739962° |
| [3,3,10/3] | degpy | 60° | 60° | 72° | arccos[(sqrt(5)-2)/3] = 85.486768° |
arccos[(5-sqrt(5))/6] = 62.570597° |
arccos[(5-sqrt(5))/6] = 62.570597° |
| [3,4,4] | trip | 60° | 90° | 90° | 90° | 90° | 60° |
| [3,4,5] | 60° | 90° | 108° | arccos(-sqrt[(3-sqrt(5))/6]) = 110.905157° |
arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
arccos(sqrt[(5-sqrt(5))/10]) = 58.282526° |
|
| [3,4,5/2] | 60° | 90° | 36° | arccos(sqrt[(3+sqrt(5))/6]) = 20.905157° |
arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(sqrt[(5+sqrt(5))/10]) = 31.717474° |
|
| [3,4,6] | tricu | 60° | 90° | 120° | arccos[-1/sqrt(3)] = 125.264390° |
arccos(1/3) = 70.528779° |
arccos[1/sqrt(3)] = 54.735610° |
| [3,4,8] | squacu | 60° | 90° | 135° | arccos[-sqrt(2/3)] = 144.735610° |
arccos[1/sqrt(3)] = 54.735610° |
45° |
| [3,4,8/3] | rasquacu | 60° | 90° | 45° | arccos(sqrt(2/3)) = 35.264390° |
arccos[-1/sqrt(3)] = 125.264390° |
45° |
| [3,4,10] | pecu | 60° | 90° | 144° | arccos(-sqrt[(3+sqrt(5))/6]) = 159.094843° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
arccos(sqrt[(5+sqrt(5))/10]) = 31.717474° |
| [3,4,10/3] | rastacu | 60° | 90° | 72° | arccos(sqrt[(3-sqrt(5))/6]) = 69.094843° |
arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
arccos(sqrt[(5-sqrt(5))/10]) = 58.282526° |
| [3,5,5] | teddi | 60° | 108° | 108° | arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
arccos(1/sqrt(5)) = 63.434949° |
| [3,5,10] | pero | 60° | 108° | 144° | arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
arccos(1/sqrt(5)) = 63.434949° |
| [3,5/2,5/2] | 60° | 36° | 36° | arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
arccos(-1/sqrt(5)) = 116.565051° |
|
| [3,5/2,10/3] | 60° | 36° | 72° | arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
arccos(1/sqrt(5)) = 63.434949° |
|
| [3,6,6] | tut | 60° | 120° | 120° | arccos(-1/3) = 109.471221° |
arccos(-1/3) = 109.471221° |
arccos(1/3) = 70.528779° |
| [3,6,10] | 60° | 120° | 144° | arccos(-sqrt(5)/3) = 138.189685° |
arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
|
| [3,6,10/3] | 60° | 120° | 72° | arccos(sqrt(5)/3) = 41.810315° |
arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
|
| [3,8,8] | tic | 60° | 135° | 135° | arccos[-1/sqrt(3)] = 125.264390° |
arccos[-1/sqrt(3)] = 125.264390° |
90° |
| [3,8/3,8/3] | quith | 60° | 45° | 45° | arccos[1/sqrt(3)] = 54.735610° |
arccos[1/sqrt(3)] = 54.735610° |
90° |
| [3,10,10] | tid | 60° | 144° | 144° | arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(-1/sqrt(5)) = 116.565051° |
| [3,10/3,10/3] | quit gissid | 60° | 72° | 72° | arccos(arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
arccos(arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
arccos(1/sqrt(5)) = 63.434949° |
| [4,4,4] | cube | 90° | 90° | 90° | 90° | 90° | 90° |
| [4,4,5] | pip | 90° | 90° | 108° | 108° | 90° | 90° |
| [4,4,5/2] | stip | 90° | 90° | 36° | 36° | 90° | 90° |
| [4,4,6] | hip | 90° | 90° | 120° | 120° | 90° | 90° |
| [4,4,8] | op | 90° | 90° | 135° | 135° | 90° | 90° |
| [4,4,8/3] | stop | 90° | 90° | 45° | 45° | 90° | 90° |
| [4,4,10] | dip | 90° | 90° | 144° | 144° | 90° | 90° |
| [4,4,10/3] | stiddip | 90° | 90° | 72° | 72° | 90° | 90° |
| [4,5,5/2] | 90° | 108° | 36° | arccos(sqrt[(5+sqrt(5))/10]) = 31.717474° |
arccos(-sqrt[(5-sqrt(5))/10]) = 121.717474° |
arccos(1/sqrt(5)) = 63.434949° |
|
| [4,5,6] | 90° | 108° | 120° | arccos(-sqrt[(5-sqrt(5))/10]) = 121.717474° |
arccos(-sqrt[(3-sqrt(5))/6]) = 110.905157° |
arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
|
| [4,5,10] | dirid | 90° | 108° | 144° | arccos(-sqrt[(5+sqrt(5))/10]) = 148.282526° |
arccos(-sqrt[(5-sqrt(5))/10]) = 121.717474° |
arccos(-1/sqrt(5)) = 116.565051° |
| [4,5/2,6] | 90° | 36° | 120° | arccos(-sqrt[(5+sqrt(5))/10]) = 148.282526° |
arccos(sqrt[(3+sqrt(5))/6]) = 20.905157° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
|
| [4,5/2,10/3] | 90° | 36° | 72° | arccos(sqrt[(5-sqrt(5))/10]) = 58.282526° |
arccos(sqrt[(5+sqrt(5))/10]) = 31.717474° |
arccos(-1/sqrt(5)) = 116.565051° |
|
| [4,6,6] | toe | 90° | 120° | 120° | arccos[-1/sqrt(3)] = 125.264390° |
arccos[-1/sqrt(3)] = 125.264390° |
arccos(-1/3) = 109.471221° |
| [4,6,8] | girco | 90° | 120° | 135° | arccos[-sqrt(2/3)] = 144.735610° |
135° | arccos[-1/sqrt(3)] = 125.264390° |
| [4,6,8/3] | quitco | 90° | 120° | 45° | arccos(sqrt(2/3)) = 35.264390° |
135° | arccos[1/sqrt(3)] = 54.735610° |
| [4,6,10] | grid | 90° | 120° | 144° | arccos(-(1+sqrt(5))/sqrt(12)) = 159.094843° |
arccos(-sqrt[(5+sqrt(5))/10]) = 148.282526° |
arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
| [4,6,10/3] | gaquatid | 90° | 120° | 72° | arccos(sqrt[(3-sqrt(5))/6]) = 69.094843° |
arccos(-sqrt[(5-sqrt(5))/10]) = 121.717474° |
arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
| [4,10,10/3] | quitdid | 90° | 144° | 72° | arccos(sqrt[(5-sqrt(5))/10]) = 58.282526° |
arccos(-sqrt[(5+sqrt(5))/10]) = 148.282526° |
arccos(1/sqrt(5)) = 63.434949° |
| [5,5,5] | doe | 108° | 108° | 108° | arccos(-1/sqrt(5)) = 116.565051° |
arccos(-1/sqrt(5)) = 116.565051° |
arccos(-1/sqrt(5)) = 116.565051° |
| [5,5/2,6] | 108° | 36° | 120° | arccos(-1/sqrt(5)) = 116.565051° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
|
| [5,6,6] | ti | 108° | 120° | 120° | arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(-sqrt(5)/3) = 138.189685° |
| [5,6,10/3] | 108° | 120° | 72° | arccos(sqrt[(5-2 sqrt(5))/15]) = 79.187683° |
arccos(-1/sqrt(5)) = 116.565051° |
arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
|
| [5,10/3,10/3] | quit sissid | 108° | 72° | 72° | arccos(1/sqrt(5)) = 63.434949° |
arccos(1/sqrt(5)) = 63.434949° |
arccos(-1/sqrt(5)) = 116.565051° |
| [5/2,5/2,5/2] | gissid | 36° | 36° | 36° | arccos(1/sqrt(5)) = 63.434949° |
arccos(1/sqrt(5)) = 63.434949° |
arccos(1/sqrt(5)) = 63.434949° |
| [5/2,6,6] | tiggy | 36° | 120° | 120° | arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
arccos(sqrt(5)/3) = 41.810315° |
| [5/2,6,10] | 36° | 120° | 144° | arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(1/sqrt(5)) = 63.434949° |
arccos(sqrt[(5+2 sqrt(5))/15]) = 37.377368° |
|
| [5/2,10,10] | tigid | 36° | 144° | 144° | arccos(-1/sqrt(5)) = 116.565051° |
arccos(-1/sqrt(5)) = 116.565051° |
arccos(1/sqrt(5)) = 63.434949° |
| [6,8,8/3] | cotco | 120° | 135° | 45° | arccos[1/sqrt(3)] = 54.735610° |
arccos[-1/sqrt(3)] = 125.264390° |
90° |
| [6,10,10/3] | idtid | 120° | 144° | 72° | arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° |
arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° |
arccos(-1/sqrt(5)) = 116.565051° |
| ... * | |||||||
* Infact, except for the there missing acrons [3,5,6], [3,5,8], [3,5,8/3], [3,5,10/3], [3,5/2,8/3], [3,6,8], [3,8,10], [3,8/3,10/3], [4,5,5], [4,5,8], [4,5,8/3], [4,5,10/3], [4,8,10/3], [4,8/3,10/3], [4,10/3,10/3], [5,5,5/2], [5,5,6], [5,5,8], [5,5,8/3], [5,5,10/3], [5,6,8/3], [5,8,8/3], [5,8,10/3], [5,8/3,10], [5,8/3,10/3], [5,10,10/3], [5/2,5/2,8/3], [5/2,6,8], [5/2,8,8], [5/2,8,10], [5/2,8/3,8/3], [5/2,8/3,10/3], [5/2,10/3,10/3], [6,6,8/3], [6,6,10/3], [6,8,10/3], [6,8/3,10], [6,10/3,10/3], [8,8,8/3], [8,8,10/3], [8,8/3,10], [8,10,10/3], [8,10/3,10/3], [8/3,8/3,8/3], [8/3,8/3,10/3], [8/3,10,10], and [10/3,10/3,10/3] those are all possible trihedral cases using polygons {3}, {4}, {5}, {5/2}, {6}, {8}, {8/3}, {10}, and {10/3} only: Any of these missing acrons would ask for dihedral angles not provided by the finite symmetry groups directly.
---- 4D ----
In 4D 'dihedral angles' sometimes are better referenced as dichoral angles, as those truely measure the angle between 2 chora (facet polytopes) of a polychoron. None the less 'dihedral angle' is the more wide spread term, then being applied dimensionally independently, and thus just extrapolating the 3D setup.
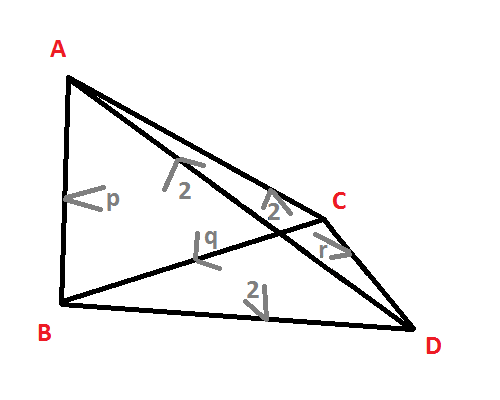
The dual of the orthoscheme of this dimension is known as Goursat tetrahedron. – To the right (and in the followings) the orthoscheme according to symmetry o-p-o-q-o-r-o will be considered. The face, derived by kaleidoscopical construction around vertex A clearly is of subsymmetry o-p-o . o, corresponds thus to the omission of the (zero-based) node number 2. By symmetry vertex D corresponds to subsymmetry o . o-r-o, i.e. to omission of node 1. The vertex B then corresponds to subsymmetry o-p-o-q-o ., or the omission of node 3. Again by symmetry C corresponds to . o-q-o-r-o, or node 0.
Consideration of tiny surroundings at the vertices of the corresponding hyperspherical orthoscheme ABCD will derive the 12 corner angles of the facing spherical triangles again by the law of cosines, which relates the 3 corner angles U,V,W to the opposite sides u,v,w by cos(U) = - cos(V) cos(W) + sin(V) sin(W) cos(u).
Thus around vertex A we derive directly (in terms of the Dynkin link marks p,q,r, respectively in terms of the above shortchord
definitions P,Q,R):
cos(∠BAC) =
[cos(π/2) + cos(π/p) cos(π/2)] / [sin(π/p) sin(π/2)] =
0
cos(∠BAD) =
[cos(π/2) + cos(π/2) cos(π/p)] / [sin(π/2) sin(π/p)] =
0
cos(∠CAD) =
[cos(π/p) + cos(π/2) cos(π/2)] / [sin(π/2) sin(π/2)] =
cos(π/p) =
sqrt(P / 4)
(And by symmetry the similar result for vertex D.)
Around vertex B we similarily derive:
cos(∠ABC) =
[cos(π/2) + cos(π/p) cos(π/q)] / [sin(π/p) sin(π/q)] =
cot(π/p) cot(π/q) =
sqrt[Q / (4 - P)] sqrt[P / (4 - Q)]
cos(∠ABD) =
[cos(π/q) + cos(π/2) cos(π/p)] / [sin(π/2) sin(π/p)] =
cos(π/q) / sin(π/p) =
sqrt[Q / (4 - P)]
cos(∠CBD) =
[cos(π/p) + cos(π/q) cos(π/2)] / [sin(π/q) sin(π/2)] =
cos(π/p) / sin(π/q) =
sqrt[P / (4 - Q)]
(And by symmetry the similar result for vertex C.)
By use of those corner angles (and the same formula as above) one thus derives the arc lengths of the "edges" of that
spherical simplex:
E.g. using triangle ABD we get:
cos(β(2,3)) =
cos(AB) =
[cos(∠ADB) + cos(∠BAD) cos(∠ABD)] / [sin(∠BAD) sin(∠ABD)] =
sqrt((4 - P) / 4) sqrt[R / (4 - P - Q)]
cos(β(1,2)) =
cos(AD) =
[cos(∠ABD) + cos(∠ADB) cos(∠BAD)] / [sin(∠ADB) sin(∠BAD)] =
sqrt[Q / (4 - R)] sqrt[4 / (4 - P)]
cos(β(1,3)) =
cos(BD) =
[cos(∠BAD) + cos(∠ABD) cos(∠ADB)] / [sin(∠ABD) sin(∠ADB)] =
sqrt[Q / (4 - R)] sqrt[R / (4 - P - Q)]
(where the numbers refer to the facetal directions associated within paragraph 2).
And by symmetry the similar result using triangle ACD:
cos(β(0,1)) =
cos(CD) =
sqrt((4 - R) / 4) sqrt[P / (4 - Q - R)]
cos(β(1,2)) again (above formula obviously being symmetric in P and R)
cos(β(0,2)) =
cos(AC) =
sqrt[Q / (4 - P)] sqrt[P / (4 - Q - R)]
For the so far missing case β(0,3) one equally could use triangle ABC or BCD:
cos(β(0,3)) =
cos(BC) =
[cos(∠BAC) + cos(∠ABC) cos(∠ACB)] / [sin(∠ABC) sin(∠ACB)] =
sqrt[Q / 4] sqrt[P / (4 - Q - R)] sqrt[R / (4 - P - Q)],
obviously an expression which is symmetrical in P and R.
Finally we generally use
cos(α(0,0')) =
- cos(β(0,0')) =
- cos(2 β(0,1)) =
- [2 cos2(β(0,1)) - 1] =
1 - 2 [(4 - R) / 4] [P / (4 - Q - R)], resp.
cos(α(3,3')) =
- cos(β(3,3')) =
- cos(2 β(2,3)) =
- [2 cos2(β(2,3)) - 1] =
1 - 2 [(4 - P) / 4] [R / (4 - P - Q)].
| Symmetry o-p-o-q-o-r-o |
centri angles | dihedral angles (& regular example) | ||||||
|---|---|---|---|---|---|---|---|---|
| p | q | r | β(0,0') | β(3,3') | α(0,0') = ∠ . o-q-o-r-o, . o-q-o-r-o | α(3,3') = ∠ o-p-o-q-o ., o-p-o-q-o . | ||
| 3 | 3 | 3 | arccos(-1/4) = 104.477512° |
arccos(-1/4) = 104.477512° |
arccos(1/4) = 75.522488° |
pen | arccos(1/4) = 75.522488° |
pen |
| 3 | 3 | 4 | 90° | 60° | 90° | tes | 120° | hex |
| 3 | 4 | 3 | 60° | 60° | 120° | ico | 120° | ico |
| 3 | 3 | 5 | 36° | arccos[(1+3 sqrt(5))/8] = 15.522488° |
144° | hi | arccos[-(1+3 sqrt(5))/8] = 164.477512° |
ex |
| 3 | 3 | 5/2 | 108° | arccos[-(3 sqrt(5)-1)/8] = 135.522488° |
72° | gogishi | arccos[(3 sqrt(5)-1)/8] = 44.477512° |
gax |
| 3 | 5 | 5/2 | 36° | 60° | 144° | sishi | 120° | fix |
| 3 | 5/2 | 5 | 108° | 60° | 72° | gaghi | 120° | gofix |
| 5 | 3 | 5/2 | 36° | 108° | 144° | gishi | 72° | gahi |
| 5 | 5/2 | 5 | 36° | 36° | 144° | gohi | 144° | gohi |
| 5/2 | 5 | 5/2 | 108° | 108° | 72° | gashi | 72° | gashi |
| ... | ||||||||
| Symmetry o-p-o-q-o-r-o |
centri angles (continued) | |||||||
| p | q | r | β(0,1) | β(0,2) | β(0,3) | β(1,2) | β(1,3) | β(2,3) |
| 3 | 3 | 3 | arccos(sqrt[3/8]) = 52.238756° |
arccos(sqrt[1/6]) = 65.905157° |
arccos(1/4) = 75.522488° |
arccos(2/3) = 48.189685° |
arccos(sqrt[1/6]) = 65.905157° |
arccos(sqrt[3/8]) = 52.238756° |
| 3 | 3 | 4 | 45° | arccos[1/sqrt(3)] = 54.735610° |
60° | arccos(sqrt[2/3]) = 35.264390° |
45° | 30° |
| 3 | 4 | 3 | 30° | arccos(sqrt[2/3]) = 35.264390° |
45° | arccos(sqrt[8/9]) = 19.471221° |
arccos(sqrt[2/3]) = 35.264390° |
30° |
| 3 | 3 | 5 | 18° | arccos(sqrt[(3+sqrt(5))/6]) = 20.905157° |
arccos(sqrt[7+3 sqrt(5)]/4) = 22.238756° |
arccos(sqrt[(10+2 sqrt(5))/15]) = 10.812317° |
arccos(sqrt[(5+2 sqrt(5))/10]) = 13.282526° |
arccos(sqrt[9+3 sqrt(5)]/4) = 7.761244° |
| ... | ||||||||
| Symmetry o-p-o-q-o-r-o |
dihedral angles (continued) | |||||||
| p | q | r | α(0,1) = ∠ . o-q-o-r-o, o . o-r-o |
α(0,2) = ∠ . o-q-o-r-o, o-p-o . o |
α(0,3) = ∠ . o-q-o-r-o, o-p-o-q-o . |
α(1,2) = ∠ o . o-r-o, o-p-o . o |
α(1,3) = ∠ o . o-r-o, o-p-o-q-o . |
α(2,3) = ∠ o-p-o . o, o-p-o-q-o . |
| 3 | 3 | 3 | arccos[-sqrt(3/8)] = 127.761244° |
arccos[-1/sqrt(6)] = 114.094843° |
arccos(-1/4) = 104.477512° |
arccos(-2/3) = 131.810315° |
arccos[-1/sqrt(6)] = 114.094843° |
arccos[-sqrt(3/8)] = 127.761244° |
| 3 | 3 | 4 | 135° | arccos[-1/sqrt(3)] = 125.264390° |
120° | arccos[-sqrt(2/3)] = 144.735610° |
135° | 150° |
| 3 | 4 | 3 | 150° | arccos[-sqrt(2/3)] = 144.735610° |
135° | arccos(-sqrt[8/9]) = 160.528779° |
arccos[-sqrt(2/3)] = 144.735610° |
150° |
| 3 | 3 | 5 | 162° | arccos(-sqrt[(3+sqrt(5))/6]) = 159.094843° |
arccos(-sqrt[7+3 sqrt(5)]/4) = 157.761244° |
arccos(-sqrt[(10+2 sqrt(5))/15]) = 169.187683° |
arccos(-sqrt[(5+2 sqrt(5))/10]) = 166.717474° |
arccos(-sqrt[9+3 sqrt(5)]/4) = 172.238756° |
| ... | ||||||||
In the special case of duoprismatic symmetries we'd just get q=2 and hence Q=0 within the above derivation. Esp.
cos(β(0,1)) = sqrt(P / 4) = cos(π/p),
cos(β(2,3)) = sqrt(R / 4) = cos(π/r),
cos(β(0,2)) = cos(β(0,3)) = cos(β(1,2)) = cos(β(1,3)) = 0 = cos(π/2).
Within the other special case of (mono-) prismatic symmetries we'd just get say r=2 and hence R=0
in the above derivation. Esp.
cos(β(0,3)) = cos(β(1,3)) = cos(β(2,3)) = 0 = cos(π/2),
cos(β(0,1)) = sqrt(P / (4 - Q)),
cos(β(1,2)) = sqrt(Q / (4 - P)),
cos(β(0,2)) = sqrt(P / (4 - Q)) sqrt(Q / (4 - P)),
where the latter 3 values just reproduce those of the prism base polyhedron.
From this proof it follows that the only fundamental case here is o3o3o *b3o.
Thus in contrast to the provided setup for the linear diagrams we now would have:
all the dihedral angles of the orthoscheme emanating from vertex A are π/2 whereas all other dihedral angles are π/3.
Next we have to determine the according corner angles of the associated triangles. Here we get:
cos(∠BAC) =
cos(∠BAD) =
cos(∠CAD) =
[cos(π/2) + cos(π/2) cos(π/2)] / [sin(π/2) sin(π/2)] =
0
cos(∠ABC) =
cos(∠ACB) =
cos(∠ABD) =
cos(∠ADB) =
cos(∠ACD) =
cos(∠ADC) =
[cos(π/3) + cos(π/2) cos(π/3)] / [sin(π/2) sin(π/3)] =
1/sqrt(3) =
sqrt(1 / (4 - 1))
cos(∠BCD) =
cos(∠CDB) =
cos(∠DBC) =
[cos(π/2) + cos(π/3) cos(π/3)] / [sin(π/3) sin(π/3)] =
1/3 =
sqrt(1 / (4 - 1)) sqrt(1 / (4 - 1))
For the remainder we first have to associate again the facet directions to the corners of the orthoscheme, i.e. to the ones of the here relevant Goursat tetrahedron. Obviously A is associated to the symmetry of the Dynkin subdiagram with omission of the central node, i.e. o . o o. Corners B, C, and D here are equivalent and thus might be associated to subsymmetries o3o3o ., to o3o . *b3o, and to . o3o *b3o. When we again associate numbers to these subsymmetries according to the (zero based) ommited node in that linearization, then the cell around D would be "0", that around A would be "1", that around C would be "2", and that around B would be "3".
Next we derive the edge lengths of the orthoscheme and thus the angles wrt. the body center β(i,j), e.g. by inspectation of triangle ABC:
cos(β(1,3)) =
cos(AB) =
[cos(∠ACB) + cos(∠BAC) cos(∠ABC)] / [sin(∠BAC) sin(∠ABC)] =
1/sqrt(2) =
sqrt(1 / (4 - 1 - 1))
cos(β(2,3)) =
cos(BC) =
[cos(∠BAC) + cos(∠ABC) cos(∠ACB)] / [sin(∠ABC) sin(∠ACB)] =
1/2 =
sqrt(1 / (4 - 1 - 1)) sqrt(1 / (4 - 1 - 1))
And by symmetry we further have:
cos(β(1,2)) =
cos(AC) =
1/sqrt(2)
cos(β(0,1)) =
cos(AD) =
1/sqrt(2)
cos(β(0,3)) =
cos(BD) =
1/2
cos(β(0,2)) =
cos(CD) =
1/2
Therefore we derive the according angles β(i,j) directly as well as the complemental dihedral ones α(i,j) as:
β(0,2) =
arccos(1/2) =
60°
β(0,3) =
arccos(1/2) =
60°
β(2,3) =
arccos(1/2) =
60°
β(0,1) =
arccos(1/sqrt(2)) =
45°
β(1,2) =
arccos(1/sqrt(2)) =
45°
β(1,3) =
arccos(1/sqrt(2)) =
45°
α(0,2) =
arccos(-1/2) =
120°
α(0,3) =
arccos(-1/2) =
120°
α(2,3) =
arccos(-1/2) =
120°
α(0,1) =
arccos(-1/sqrt(2)) =
135°
α(1,2) =
arccos(-1/sqrt(2)) =
135°
α(1,3) =
arccos(-1/sqrt(2)) =
135°
Like for the linear diagram we well have the straight angle associates at 2 adjoined orthoschemes here too, providing:
cos(α(0,0')) =
-cos(β(0,0')) =
-cos(2β(0,1)) =
-cos(90°) =
0
and thus, by symmetry, 90° = α(0,0') = α(2,2') = α(3,3') = β(0,0') = β(2,2') = β(3,3').
An alternate derivation of dihedral angles is based on a localised and hierarchical access, which calculates angles across ridges (D-2 elements) between pairs of margins (D-1 elements) of some D-dimensional polytope around any threefold (and thus rigid) peak (D-3 elements) of it. This is based on the spherical law of cosines (for sides) cos(c) = cos(a) cos(b) + sin(a) sin(b) cos(γ), which solves to γ = arccos[(cos(c) - cos(a) cos(a)) / sin(a) sin(b)].
Here the above γ would result in the searched for dihedral angle αD of the D-dimensional polytope (at the considered ridge). And a,b,c represent the respective dihedral angles αD-1 of the there incident D-1-dimensinal margin polytopes.
Esp. when all dihedral angles a = αD-1 generally are provided by some algebraic expressions, i.e. cos(αD-1) = [algebr. expr.], terms like cos(a) are immediate. For the used terms sin(a) we'd thus get sin(a) = sin(arccos([algebr. expr.])) = sqrt(1 - [algebr. expr.]2). (Sign issues do not intervene here, at least as long as only dihedral angles αD-1 < π will be involved. But this is just the domain of arccos. Therefore we will be safe here.)
Thus, if A,B,C are such algebraic expressions for cosines of incident dihedral angles αD-1, i.e. A = cos(a) etc., and still C will be the one opposite to the searched for dihedral angle αD, then we thus derive αD = arccos[ (C - A B) / sqrt[(1 - A2)(1 - B2)] ].
Thus this formula is ready for application whenever threefold peaks occur and all 3 subdimensional dihedral angles are known. Applied to polyhedra, then ridges are edges, and peaks are vertices. Thus this formula in fact was used in the section on rigid acrons already. – Applied to polychora, then ridges are polygons, and peaks are edges. According applications will be spread throughout several incmats-files, though not listed here. (Examples would be according calculations for segmentochora which are not directly associated to Wythoff's kaleidoscopic construction via segmental cut outs.)
Any dimensional regular polytope {p, q, r, ..., s} = x-p-o-q-o-r-o-...-o-s-o could be solved recursively by means of the following observation. On the one side we had derived above already the dihedral angle for any such regular polyhedron, e.g. in the form:
α({p, q}) = 2 arcsin[ cos(π/q) / sin(π/p) ]
For the internal corner angle of a regular n-gon {n} on the other hand one clearly has
ϕ({n}) = π (1 - 2/n)
The idea now runs as follows. Reduce the length of the Schläfli symbol {p, q, r, ..., s} iteratively by one, combining its first 2 numbers into a single one instead: {n(p, q), r, ..., s}. Here n(p, q) then simply describes that numerical value, which corrsponds to ϕ({n}) = α({p,q}). This therefore results in
n(p, q) = ϕ-1(α({p, q})) = π/(π/2 - arcsin[ cos(π/q) / sin(π/p) ]) = π/arccos[ cos(π/q) / sin(π/p) ]
In fact this idea simply searches for that 2D n-gon (n now being generally an arbitrary positive real number for sure), which has the same internal corner angle as the dihedral angle of the originally being used 3D cell {p, q}. And thereafter replacing that number in the former Schläfli symbol instead.
Thence we derive the following recursion rule
α({p, q, r, ..., s}) = α({ n(p, q) , r, ..., s}) = α({ n[ n(p, q), r] , ..., s}) = ... = ϕ( {n(n(...n(n(p, q), r), ...), s)} )
© 2004-2025 | top of page |