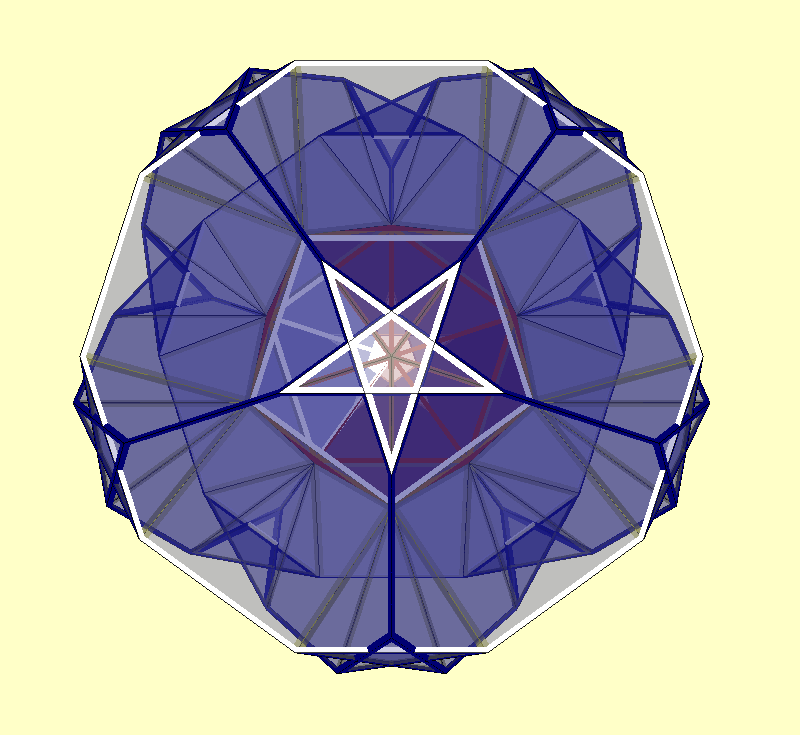
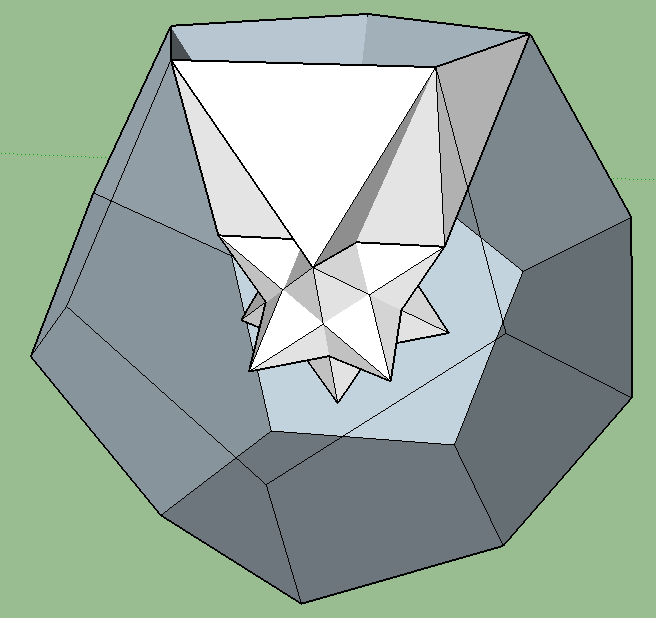
Closed Finite Flat Complexes

There are 2 opposite paths which lead to closed finite flat complexes, i.e. adjoins of polytopes, which then finally are closed with respect to the dihedrality rule, thereby completely remaining within euclidean space of component dimension: On the one hand those are produced bottom-up as continually growing complexes, which finally allow for a closure by means of a not completely coincident second such. Esp. (but not necessary) whenever that second one happens to be a single larger polytope. On the other hand those are derived as degenerate cases of higher dimensional polytopes, when the height between consecutive layers evaluates to zero.

The former sense can be found in the extraction of finite patches of euclidean tesselations.
The second pathway e.g. is used by degenerate segmentotopes.

Esp. in the former sense, there come in some unusual additions: besides of locally finite euclidean reflection groups there are also locally dense ones. Those are usually rejected right for that reason. But here, when using only finite patches (which somehow can be closed dihedrally for sure), all those groups come back into play! Just because of using only finite complexes therefrom, and therefore this displeasing density does not show up here already.

With respect to the dihedral angles we get the restriction, that either (in the interior) those of the incident components will add directly to 360° (as for tesselations), or (at the boarder) a subset of those component angles would add to some value, which by the angles of the complemental subset would be exhausted again. In cases of a complete decomposition the choice of that former subset is obvious.

There is neither a firm definition nor a completed research to this subject. This page rather serves as an attempt of a temporary collection.

• dimension 2
• dimension 3
• dimension 4

----
 2D
----

Locally dense groups

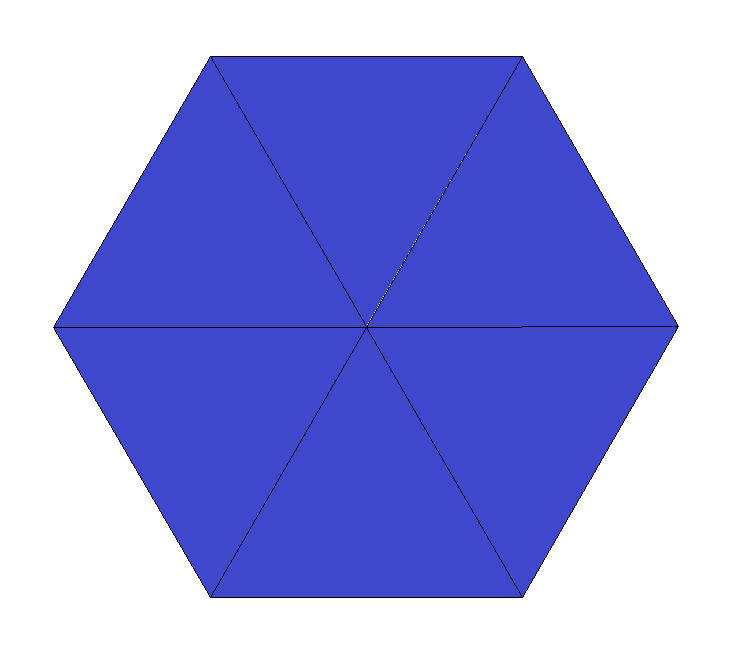
For locally 2D polytopal manifolds oPoQoR*a the restriction to euclidean geometry amounts to 1/P + 1/Q + 1/R = 1. For R = 2 this then just resolves to Q = 2P/(P-2). Therefore we might consider all the following (linear symbol) groups:

o3o6o      (locally finite)
o4o4o      (locally finite)
o5o10/3o   (locally dense)
o5/2o10o   (locally dense)
o6o3o      (locally finite)
o7o14/5o   (locally dense)
o7/2o14/3o (locally dense)
o7/3o14o   (locally dense)
o8o8/3o    (locally dense)
o9o18/7o   (locally dense)
o9/2o18/5o (locally dense)
o9/4o18o   (locally dense)
...

Flat Segmentohedra

pt || {6}   = ox6oo&#x
  = hippy
{6} || {12} = ox6xx&#x
  = hicu

pt || pseudo {6} || {12}       = oxx6oox&#xt
{6} || pseudo {12} || dual {6} = xxo6oxx&#xt

{3/2}-ap = ss3/2ss&#x
  = trirp

top of page

----
 3D
----

Johnsonians

Several of the Johnson solids in fact are a stack (or, more general: an external blend) of elementary components. Accordingly those can serve here as a corresponding double cover too: at the one hand just that composition of components, on the other one right the resulting solid. – Similarily also some uniform or even regular ones can be decomposed using Johnson solids as (some of their) elements.

2x tet          = tridpy (J12)
2x squippy (J1) = oct (regular)
2x peppy (J2)   = pedpy (J13)
2x tricu (J3)   = co (uniform)
2x tricu (J3)   = tobcu (J27)
2x pero (J6)    = id (uniform)
2x pero (J6)    = pobro (J34)

tet + trip      = etripy (J7)
squippy + cube  = esquipy (J8)
peppy + pip     = epeppy (J9)
squippy + squap = gyesp (J10)
peppy + pap     = gyepip (J11)
peppy + mibdi (J62)    = gyepip (J11)
2x peppy + teddi (J63) = gyepip (J11)

4x tet + 3x squippy    = tricu (J3)
2x squippy + squap     = gyesqidpy (J17)
2x peppy + pap         = ike (regular)
2x peppy + mibdi (J62) = ike (regular)
3x peppy + teddi (J63) = ike (regular)
3x squippy + trip      = tautip (J51)
2x squacu (J4) + op    = sirco (uniform)
2x squacu (J4) + op    = esquigybcu (J37)

...

 ©

Toroids

A related research, digging tunnels through larger polyhedra, was published as "Adventures Among the Toroids" by Stewart. There he restricts to larger convex polyhedra, being tunneled by smaller polyhedra. Further excluding thereby intersecting faces.

(In fact, re-introducing the missing cells, which were defining all these tunnels, then would provide corresponding closed finite flat complexes again.)

A nice collection of those toroids is outlined by McNeill at this link. According VRMLs also are linked by courtesy of him. – A further one was found at this link written up by Doskey. (On that page he further classifies into linear, planar, and spherical dissections when refering to Johnsonians which can be seen as lace towers, to prisms of the 2D decompositions, resp. to the ones defined by toroids.)

In the context of toroids for historical reasons some special abbreviations are in use for building components, which (except of Steward's finds, G3 and Z4) generally are known otherwise:

 ©

 ©

 ©

In cases of more complex interior structures the central element then is given in parantheses and counts are used as numeric prefixes for lacing structures.

Q3P6 \ P3Q3     = xxx3oxx&#xt \ xxx3oox&#xt
Q3Q3 \ S3S3     = xxx3oxo&#xt \ xox3oxo&#xt
E4 \ B4P4       = xxxx4oxxo&#xt \ xxox4ooqo&#xt
T4 \ Q4P4Q4     = xwwx4xoox&#xt \ xxxx4xoox&#xt  (esp.: tic = ext. blend of 1 cube + 8 tets + 6 squacues)
Q4Q4 \ B4       = xxx4oxo&#xt \ xox4oqo&#xt
K3 \ Q3T3       = xuxx3xxux&#xt \ xoox3xxux&#xt
R5 \ S5Q5       = xox5ofx&#xt \ xox5oxx&#xt
Q4T4Q4 \ B4P4B4 = xxooxx4oxwwxo&#xt \ xoxxox4oqooqo&#xt
K3 \ 4Q3(S3)                                     (esp.: toe = ext. blend of 1 oct + 8 tricues + 6 squippies)
J91 \ Z4
K4 \ 12P4(E4)
K4 \ 6Q4(E4)
K4 \ 8Q3(E4)                                     (esp.: girco = ext. blend of 1 sirco + 8 tricues + 12 cubes + 6 squacues)
(more general: K4 \ aQ4 bQ3 cP4(E4) - 518 members)
K4 \ 2P4(Q4),2P4(Q4)
K4 \ 12P4(E4 \ B4P4)
E5 \ 6J91(P4)   = 8G3,12Q5                       (esp.: srid = ext. blend of 1 cube + 12 peppies + 6 bilbiros + 8 G3s
T5 \ 12Q5S5(D5)
T5 \ 6Q5S5 R5(D5)
(more general: T5 \ aQ5S5 bR5(D5))
K5 \ 12R5(E5)
...

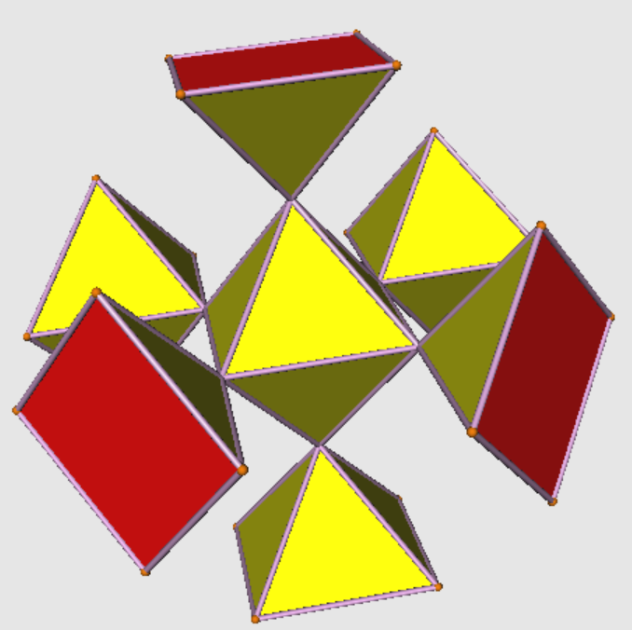©   (internal structure of the decomposition of toe)

©   (the above decomposition of srid)

A nice further toroid was found in 2019 by T. Dorozinski (cf. ©): oxFx3xfox5fovo&#zxt. It is being built from 20 thawro components only.

An other quite wild toroid, built from 6 J1, 24 J63, and 8 G3 (see above) components, was presented in 2020 in the discord forum ©. It features mostly pentagonal components in a cubical arrangement.

Locally dense groups

o3o3o *b4o     (locally finite)
o5o5/2o *b3o   (locally dense)
...

Flat Segmentochora

pt || co       = ox3oo3ox&#x
  = copy
oct || toe     = ox3xx3ox&#x
  = octatoe

tet || inv tut = ox3ox3xo&#x †)
  = tetaltut

pt || oho      = oβ3oo3ox&#x †)
  = ohopy

pt || co       = oo3ox4oo&#x
  = copy
cube || tic    = oo3ox4xx&#x
  = cubatic
oct || toe     = xx3ox4oo&#x
  = octatoe
sirco || girco = xx3ox4xx&#x
  = sircoagirco

line || hip = xx ox6oo&#x †)
  = hippyp
hip || twip = xx ox6xx&#x †)
  = hicupe

pt || did      = oo5ox5/2oo&#x
  = didpy
gad || tigid   = xx5ox5/2oo&#x
  = gaddatigid
sissid || 3doe = oo5ox5/2xx&#x
sissid || doe (i.e. reduced version of former)
  = sissidadoe

†) - The ones marked such not only are degenerate segmentotopes themselves, but would ask for subdimensional degeneracies as well.

Others

• From copy (and ohopy) it follows that chopy = pt || cho †) would belong here as well.
• From didpy it likewise follows that pt || gidhei †) and pt || sidhei †) would belong here too.

top of page

----
 4D
----

Locally dense groups

o3o3o3o3o3*a    (locally finite)
o4o3o3o4o       (locally finite)
o3o3o4o3o       (locally finite)
o3o3o *b3o4o    (locally finite)
o5o3o3o5/2o     (locally dense)
o5/2o5o3o5/2o   (locally dense)
o5o5/2o5o5/2o   (locally dense)
o5o3o5/2o5o     (locally dense)
o3o5o5/2o3o     (locally dense)
o3o3o3o3o5/2*c  (locally dense)
o3o3o3o3/2o5*c  (locally dense)
...

Flat Segmentotera

pt || spid       = ox3oo3oo3ox&#x
  = spidpy
rap || inv prip  = ox3xx3oo3ox&#x
deca || gippid   = ox3xx3xx3ox&#x

rap || inv tip   = ox3ox3xo3oo&#x †)
tip || prip      = ox3ox3xo3xx&#x †)

pen || inv srip  = xo3ox3oo3ox&#x †)
srip || inv grip = xo3ox3xx3ox&#x †)

spid || deca     = xo3ox3ox3xo&#x †)

pt || tes       = oo3oo3oo4ox&#x
  = tespy
rit || tat      = oo3oo3xx4ox&#x
ico || srit     = oo3xx3oo4ox&#x
hex || sidpith  = xx3oo3oo4ox&#x
tah || grit     = oo3xx3xx4ox&#x
rico || proh    = xx3oo3xx4ox&#x
thex || prit    = xx3xx3oo4ox&#x
tico || gidpith = xx3xx3xx4ox&#x

pt || ico       = oo3ox3oo4oo&#x
  = icopy
tes || srit     = oo3ox3oo4xx&#x
rit || tah      = oo3ox3xx4oo&#x
hex || thex     = xx3ox3oo4oo&#x
tat || grit     = oo3ox3xx4xx&#x
sidpith || prit = xx3ox3oo4xx&#x
rico || tico    = xx3ox3xx4oo&#x
proh || gidpith = xx3ox3xx4xx&#x

hex || rit      = xo3oo3ox4oo&#x †)
sidpith || tat  = xo3oo3ox4xx&#x †)
thex || tah     = xo3xx3ox4oo&#x †)
prit || grit    = xo3xx3ox4xx&#x †)

rit || thex     = ox3ox3xo4oo&#x †)
tat || prit     = ox3ox3xo4xx&#x †)

ico || rico     = ox3xo3ox4oo&#x
srit || proh    = ox3xo3ox4xx&#x

tes || sadi     = os3os3os4xo&#x

pt || ico           = ox3oo4oo3oo&#x
  = icopy
ico || spic         = ox3oo4oo3xx&#x
rico || gyro srico  = ox3oo4xx3oo&#x
rico || tico        = ox3xx4oo3oo&#x
tico || gyro prico  = ox3oo4xx3xx&#x
srico || prico      = ox3xx4oo3xx&#x
cont || grico       = ox3xx4xx3oo&#x
grico || gippic     = ox3xx4xx3xx&#xx

ico || rico         = xo3ox4oo3oo&#x
spic || srico       = xo3ox4oo3xx&#x
srico || cont       = xo3ox4xx3oo&#x
prico || gyro grico = xo3ox4xx3xx&#x

ico || sadi         = os3os4oo3xo&#x

pt || ico    = oo3ox3oo *b3oo&#x
  = icopy
hex || thex  = oo3ox3oo *b3xx&#x
rit || tah   = oo3ox3xx *b3xx&#x
rico || tico = xx3ox3xx *b3xx&#x

hex || rit   = ox3oo3ox *b3xo&#x †)
thex || tah  = ox3xx3ox *b3xo&#x †)

rit || thex  = xo3ox3xo *b3ox&#x †)

ico || rico  = ox3xo3ox *b3ox&#x

pt || tes         = ox oo3oo4ox&#x
  = tespy
oct || sircope    = ox xx3oo4ox&#x
co || ticcup      = ox oo3xx4ox&#x
toe || gircope    = ox xx3xx4ox&#x

line || perp cube = xo oo3oo4ox&#x
  = cubasc
ope  || sirco     = xo xx3oo4ox&#x
cope || tic       = xo oo3xx4ox&#x
tope || girco     = xo xx3xx4ox&#x

pt || tes            = ox4oo ox4oo&#x
  = tespy
{4} || sodip         = ox4oo ox4xx&#x
tes || odip          = ox4xx ox4xx&#x

{4} || perp {4}      = ox4oo xo4oo&#x
{8} || tes           = ox4oo xo4xx&#x
sodip || ortho sodip = ox4xx xo4xx&#x

hi || rahi       = oo3oo3ox5xo&#x
srahi || xhi     = oo3xx3ox5xo&#x
sidpixhi || srix = xx3oo3ox5xo&#x
prahi || grix    = xx3xx3ox5xo&#x

rox || hi        = oo3xo3oo5ox&#x
xhi || thi       = oo3xo3xx5ox&#x
tex || sidpixhi  = xx3xo3oo5ox&#x
grix || prix     = xx3xo3xx5ox&#x

rahi || sidpixhi = ox3oo3xo5ox&#x
xhi || prahi     = ox3xx3xo5ox&#x

rahi || tex      = ox3ox3xo5oo&#x †)
thi || prahi     = ox3ox3xo5xx&#x †)

srix || srahi    = xo3ox3xo5ox&#x

pt || gaghi        = ox5oo5/2oo3oo&#x
  = gahipy
gofix || quipdohi  = ox5oo5/2oo3xx&#x
rigfix || sirgaghi = ox5oo5/2xx3oo&#x
ragaghi || tigaghi = ox5xx5/2oo3oo&#x
tigfix || pirgaghi = ox5oo5/2xx3xx&#x

gaghi || gofix     = xo5oo5/2oo3ox&#x
sirgaghi || tigfix = xo5oo5/2xx3ox&#x

rigfix || quipdohi = ox5oo5/2xo3ox&#x

pt || sishi        = ox5/2oo5oo3oo&#x
  = sishipy
fix || padohi      = ox5/2oo5oo3xx&#x
rofix || sirsashi  = ox5/2oo5xx3oo&#x
tiffix || pirshi   = ox5/2oo5xx3xx&#x

sishi || fix       = xo5/2oo5oo3ox&#x
sirsashi || tiffix = xo5/2oo5xx3ox&#x

padohi || rofix    = xo5/2oo5ox3xo&#x

pt || sidtixhi             = ox3oo3oo3oo5/2*b&#x
  = sidtixhipy
rissidtixhi || tissidtixhi = ox3xx3oo3oo5/2*b&#x
swavixady || sphixhi       = ox3xx3xx3oo5/2*b&#x

tissidtixhi || swavixady   = xo3xx3ox3oo5/2*b&#x

sidtixhi || rissidtixhi    = xo3ox3oo3oo5/2*b&#x

pt || gidtixhi             = ox3oo3oo3/2oo5*b&#x
  = gidtixhipy
giddatady || sadtef pixady = ox3oo3oo3/2xx5*b&#x
riggidtixhi || tiggidtixhi = ox3xx3oo3/2oo5*b&#x

grawvixady || tiggidtixhi  = ox3xx3xo3/2oo5*b&#x

gidtixhi || riggidtixhi    = xo3ox3oo3/2oo5*b&#x

doe || ipe    = ox ox3oo5xo&#x
tid || tipe   = ox ox3xx5xo&#x

id || sriddip = ox ox3xo5ox&#x

ike || dope   = ox xo3oo5ox&#x
ti || tiddip  = ox xo3xx5ox&#x

iddip || srid = ox xo3ox5xo&#x

sissid || gaddip = ox ox5oo5/2xo&#x

sissiddip || gad = ox xo5oo5/2ox&#x

{5} || gyro pedip     = ox5oo ox5xo&#x
pedip || gyro padedip = ox5xx ox5xo&#x

pt || starpedip   = ox5oo ox5/2oo&#x
  = starpedippy
{5} || stardedip  = ox5xx ox5/2oo&#x

{5} || perp {5/2} = ox5oo xo5/2oo&#x
{10} || starpedip = ox5xx xo5/2oo&#x

†) - The ones marked such not only are degenerate segmentotopes themselves, but would ask for subdimensional degeneracies as well.

Others

• From the fact that both tes and ico do have unit circumradius, that tes can be decomposed into 8 cubpies, and that ico can be obtained from tes as an augmentation by such cubpies, it becomes evident that the cute will have a tip-to-tip distance of one edge unit. Thus cute itself, kind of like a 4D orange, can be decomposed into 6 squascs.
• Conversely it becomes evident that ico can be decomposed into 8 cutes. This is because for pt || ico (using here ico in the sense of an octa-augmented tes) the required cubpy-pyramids are degenerate and thus can be replaced by their own hulls.
• It finally therefrom becomes evident that this decomposition of the shape of cute into a degenerate cubasc (cubpy-pyramid) itself also belongs here. In fact, this decomposition then turns out to be the blend of the former (that "4D orange" of 6 squascs) and the trivial equatorial decomposition of cute into 2 cubpies, then thereby blending out right that cute each.
• Likewise the degenerate 8D segmentoyotton haxesc can be considered as the blend the 2 alternate decompositions of haxt: either the stack of 2 haxpies or kind a "7D orange" from 12 hinscs plus 32 ocas. In fact, this then just blends out that haxt each.
• In fact, this ambiguity between ditopal (2 polar components) and hosotopal (high-dimensional "orange") decompositions is simply based on the equatorial cross-section having a circumradius of r = sqrt(3)/2. This is not only true for cube (3D) and hax (6D), but moreover for lots of other convex uniform polytopes as well. Examples being ope (4D), dot (5D), hexip (5D), taccup (6D), tetdip (6D), geep (7D), hinsc (7D), naq (7D), roc (7D), trahix (7D), zeep (8D), ekip (9D), ...
• More general there is e.g.:
  • cute = hull of degenerate cubasc
  • haxt = hull of degenerate haxesc
  • hex = hull of degenerate {4} || perp {4}
  • gee = hull of degenerate oct || perp oct
  • naq = hull of degenerate roca
  • kadify = hull of degenerate brena
• However there even are degenerate "multistratic" lace towers of zero height as well, or alternately being seen as decompositions of the larger "base" into a central smaller "base" plus some multistratic interlacings. As examples here comes to mind the degenerate ursateron ofx3xoo3ooo5ooo&#xt (exu) and the degenerate tutsateron xux3xoo4ooo3ooo&#xt (ictum).